2 連立方程式の解き方のすべての基本! 「代入法」と「加減法」 21 連立方程式の解き方基本:加減法 22 連立方程式の解き方基本:代入法 23 連立方程式「x2y = 2xy9 = 11」の解き方 24 文字が3つ出てくる連立方程式の解き方 3 文字同士のかけ算が入る連立方程式の解き方 31 連立方程式は「いかに簡単な計算をするか」を考えよう 32 文字が2つのときの3 1 連立方程式の表現方法 連立1次方程式 (Linear Equations)は,次のような形をしている. 式 ( 7 )は行列とベクトルで書くと,式がすっきりして 考えやすくなる.書き直すと, ( 8) である.それぞれの行列とベクトルは, を表す. 通常,連立1次方程式 ( 7連立方程式 が x=y=z=0 以外の解をもつとき,実数 λ の値は次のどれか.

4d F736f F Db2cb3e6a4b8a454a4b8a440a6b8c170a5dfa4e8b57bb2d52e646f63 Pdf 免费下载
三連立方程式 サイト
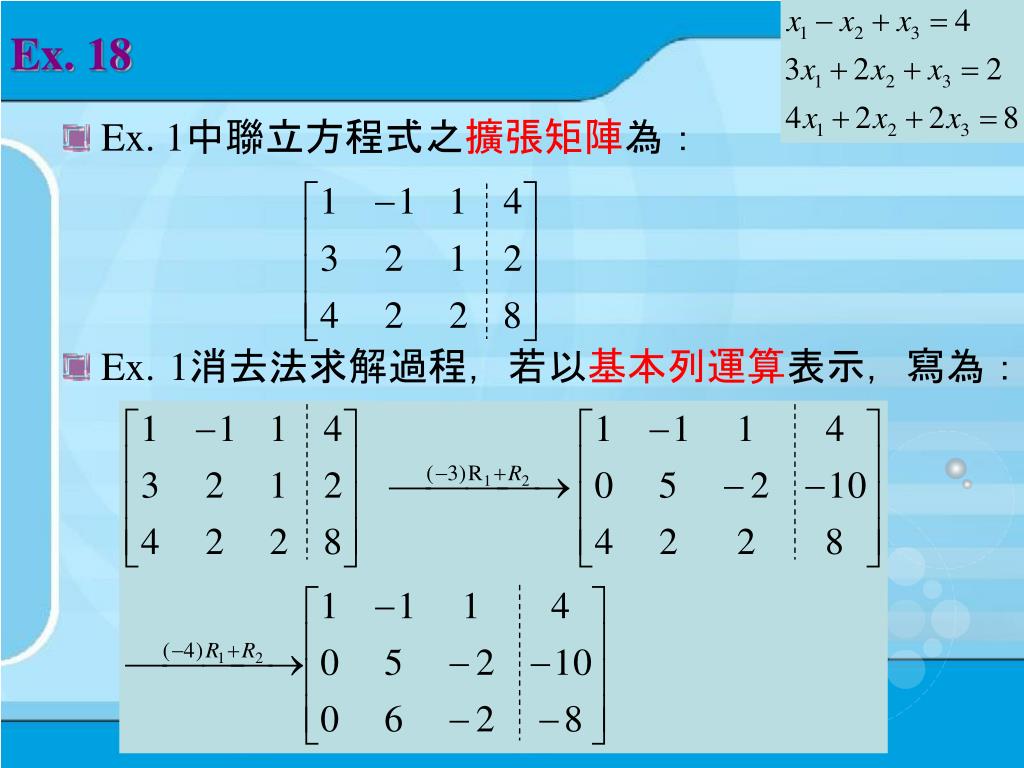
三連立方程式 サイト-3つの文字、式の連立方程式を解くためには まず、文字を1つ消してやることがポイントでしたね! そうすることで今まで解いてきた連立方程式と同じ形を作ることができます。 たくさん練習して、しっかりと手順を身につけておこうね(^^)連立 1 次方程式に基本変形をして得られた方程式と元の方程式とは等価な方程式である. すなわち両者は同じ解をもつ. 連立 1 次方程式とその行列表現は,方程式としては等価なものである. 連立 1 次方程式の基本変形は,行列表現では次の行列の行の基本変形となる. 定義 39(行列の行の基本変形) 行列に対する次の操作を行列の行の基本変形(matrix elementary row




1 兩個同時成立且並列在一起的二元一次方程式 稱為二元一次聯立方程式 Ppt Download
第三回連立方程式の解法 ガウスの消去法・行列 舟木剛 平成24年10月24日2限 数値解析‐3 1 シラバス • 授業の目的 – 工学分野でよく用いられる数値計算の算法ならびにそれらの数値的な特性について理解させる. • 授業計画 – 数値計算と誤差(1回)連立方程式の式で、 文字が片方によっている連立方程式 は代入法で解いたほうが便利なんだ。 しかも、よっている文字の係数が1ならなお最高! たとえば次のような連立方程式の問題のときだね。 例題1 つぎの連立方程式を解きなさい。 2x3y=11 y = 5x05いろいろな連立方程式 かっこのついた連立方程式中2数学 分数と小数の連立方程式中2数学 A=B=Cの連立方程式中2数学 連立方程式と解中2数学 三元連立方程式(1)中2数学 三元連立方程式(2)中2数学 06連立方程式の応用(1)
基本的な連立方程式は2つの式によるものですが、 A=B=C の形をした連立方程式もあります。 この形の連立方程式を解く場合は、 A=B=C を A=C と B=C の2つの式に分解してから加減法もしくは代入法で解きます。 2 x 7 y =3 x 5 y =22 式を分解する ① 2 x 7 y =22 ② 3 x 5 y =22 xの係数を揃える ①×3 → 6 x 21 y =66 ②×2 → 6 x 10 y =44連立方程式とは? 連立方程式(れんりつほうていしき)とは、2つ以上の方程式のことです。 下記をみてください。 これが連立方程式です。 連立方程式では、複数の未知数に対して複数の数式があります。 未知数が2つの場合、2つの式があれば解が求められます。 3つの未知数がある場合、3つの式が必要です。 ※ちなみに、これまで学習した方程式は、1つの連立方程式1 まずは加減法と代入法と呼ばれる二つのやり方を練習します。 解はすべて整数になるように作ってあります。 連立方程式2 加減法のみですが、解が分数になることもあるものです。 連立方程式3 同じく加減法で、係数が分数のものです。
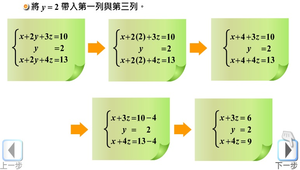
この例題の,(35)式の形に至るまで(すなわち,解がそれぞれ求まるまで)3つの演算を行う 解法を GaussJordan の消去法という.消去法は,変数の数が増えても有効な解法である. ところで,連立1次方程式(31)を行列の式で表すと連立漸化式とは? 連立漸化式とは、連立方程式のように、 異なる数列を含む複数の漸化式 です。 多くの場合、\(2\) つの数列を含む二元連立漸化式の問題が出題されます。 二元連立漸化式には、「対称型」と「一般型」があります。連立方程式とは { 7x2y = 5 2x5y = 8 のように2つ以上の方程式を組み合わせたものが 連立方程式 である。 組み合わせた, どの方程式も成り立たせるような文字の値の組が連立方程式の解となる。 中学で扱うのは上記のような2元1次方程式の連立方程式である。 2元1次方程式は1つでは解が無数にあったが,連立方程式になると (特殊な場合を除いて)解は1組である。 この



名師課輔網 100學測高斯喬登消去法




翻轉學習影片 高中 數學 三元一次聯立方程組 練習10
2次2次連立方程式を解くには,次のいずれかの型に当てはめます. (a) 一方の2次方程式が因数分解できる場合 (b) 和や差により2次の項が消去できる場合 (c) 定数項が消去できる場合 (d) 対称式にA=B=CをA=C, B=Cの形にして2つの式にする。 2x5=7x3y9 2y13=7x3y9 2x5=7x3y9を 整理して5x3y=4 2y13=7x3y9を 整理して7x5y=4 5x3y=4の両辺に5をかけ、7x5y=4の両辺に3をかけ、辺々引くと 25x15y = ) 21x15y = 12 4x = 32 両辺を4で割る連立方程式は行列計算を用い解く事ができます。さらにexcelの関数 逆行列を求める関数=minverse と 行列の積=mmultを用いればほんの数秒で解く事ができます。 それでは、以下の連立方程式を実際にexcelで解いてみましょう。
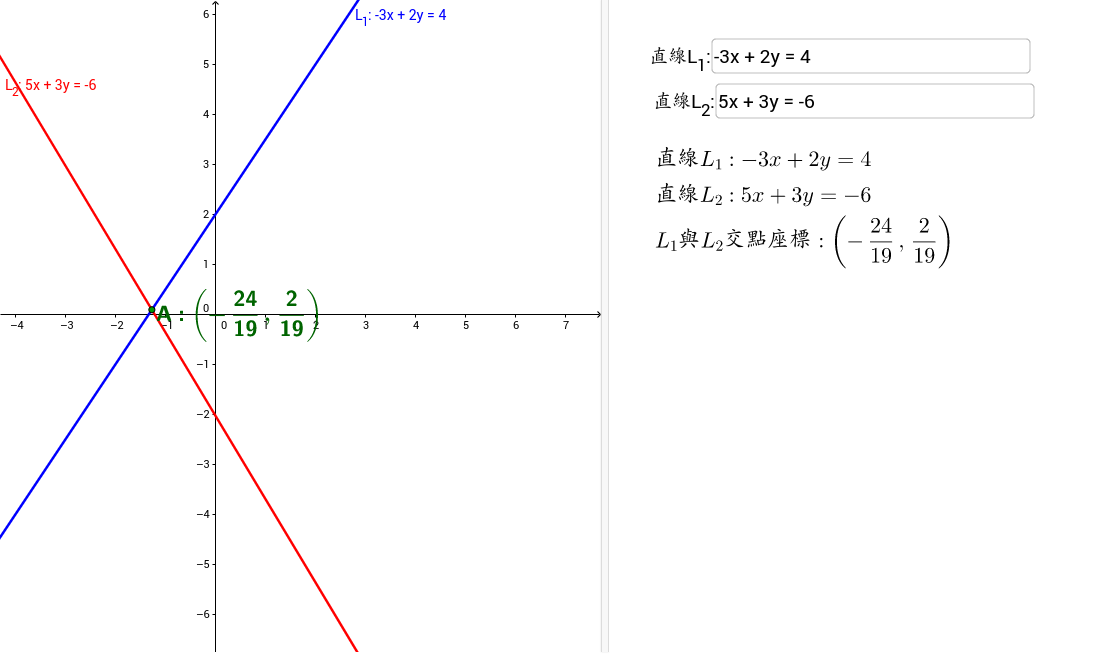



二元一次聯立方程式圖解 Geogebra




求解 這兩題我不會 Clear
連立方程式L1代入法1 2 3 4 5 連立方程式L1加減法1 2 3 4 5 6 7 8 連立方程式L2小数1 2 3 連立方程式L2分数1 2 3 4 5 6 連立方程式L3分数小数1 2 連立方程式L3分数1 2 3 4 5 6 連立A=B=C1 2 3 4 5 6 7 連立A=B=Cまとめ 連立方程式の係数1 2 3 x= 4 9, y= 5 3 x=4, y=6 x= 5 2, y= 5 4 x=2, y=4 x= 5 2, y= 3 4 a=6 式大きいほうの自然数をx, 小さい方をyとする。 xy=65 x=7y1 答連立方程式 例題 連立方程式(代入法) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(かっこのある式) 連立方程式(a=b=c) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく2元1次方程式や連立方程式の意味を理解し、代入法や加減法で、連立方程式を解く練習をする問題プリントです。 連立方程式の解き方 練習問題 (1) 答え 連立方程式の解き方 練習問題 (2) 答え 連立方程式の解き方 練習問題 (3) 答え 連立方程式の




翻轉學習影片 高中 數學 三元一次聯立方程組 練習13



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf
三角方程式を解く sin x cos x = 11 連立方程式との解き方 43 求めたx,y の値が連立方程式の解であるかどうかを確かめるには,問 1のように, もとの連立方程式の文字x,y に値を代入し,方程式が成り立つかどうかを調べればよい。 文字を1つだけふくむ方程式の解き方は1年で学んだ。連立方程式(加減法1)_ 例題と練習 連立方程式(加減法2)_ 例題と練習 連立方程式(代入法1) 連立方程式(代入法2) 連立方程式




Mathematics 数学分享站 解三元一次联立方程式 Facebook




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download
下記の3元連立1次方程式を考えよう。 (変数は x 1, x 2, x 3) 5x 1 3x 2 x 3 = 3 4x 1 5x 2 2x 3 = 4 x 1 3x 2 6x 3 = 6 とおき、マトリックスで表記すると、極めて簡単に動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru式が3つ並んでいる方程式のときには、それぞれ2つの式を組み合わせて連立方程式を作る。 \(A=B=C\) の方程式のとき $$\begin{eqnarray} \left\{ \begin{array}{l}A=B \\A=C \end{array} \right \end{eqnarray}$$




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



Http Www Powercam Cc Home Read Attach Php Id 1
やることは結局「連立方程式を解く」です。 早速、解を代入してみます。するとこの連立方程式は、 \begin{eqnarray}\left\{\begin{array}{l}4a2b=2\\4b2a=8\end{array}\right\end{eqnarray} となります。これは連立方程式と変わりませんから、同じように解いていきます。未知数の最高次数により、連立二次方程式・連立三次方程式のようによぶ。 2 (比喩的に)問題が複雑にからみ合っている物事のたとえ。「財政再建、福祉充実、景気対策の 連立方程式 を解くための政定義 28 (連立一次方程式の基本変形) 連立一次方程式に対する次のの操作を 連立一次方程式の基本変形と呼ぶ. (1) 一つの式を 倍する. (2) 二つの式を入れ替える. (3) 一つの式を 倍して別の行に加え




基礎 二元一次聯立方程式 數學 均一教育平台




隨筆誌 二下2 3三元一次聯立方程式 克拉瑪法則證明
文字が三つの式と二つの式 の連立方程式は解けますか? 例えば、3a+7b+c=85a+6b=7ということです! abcは実数だとかんがえてください 文字の個数と式の個数は同じだけ必要です。よって、 連立方程式において、3つの文字がある場合は、3つの式が必要 なわけですね。 では、例をあげながら連立方程式の3つの式を解いていきましょ1.行列で連立方程式を表すには 皆さんはこのような連立方程式の解き方を中学生のときに習ったはずです。 { 2 x − 3 y = − 5 − 3 x 4 y = 6 今回はこれを行列っぽく解いちゃいましょう。 まずは上の式を行列で書いてみます。 A = ( 2 − 3 − 3 4), x → = ( x y
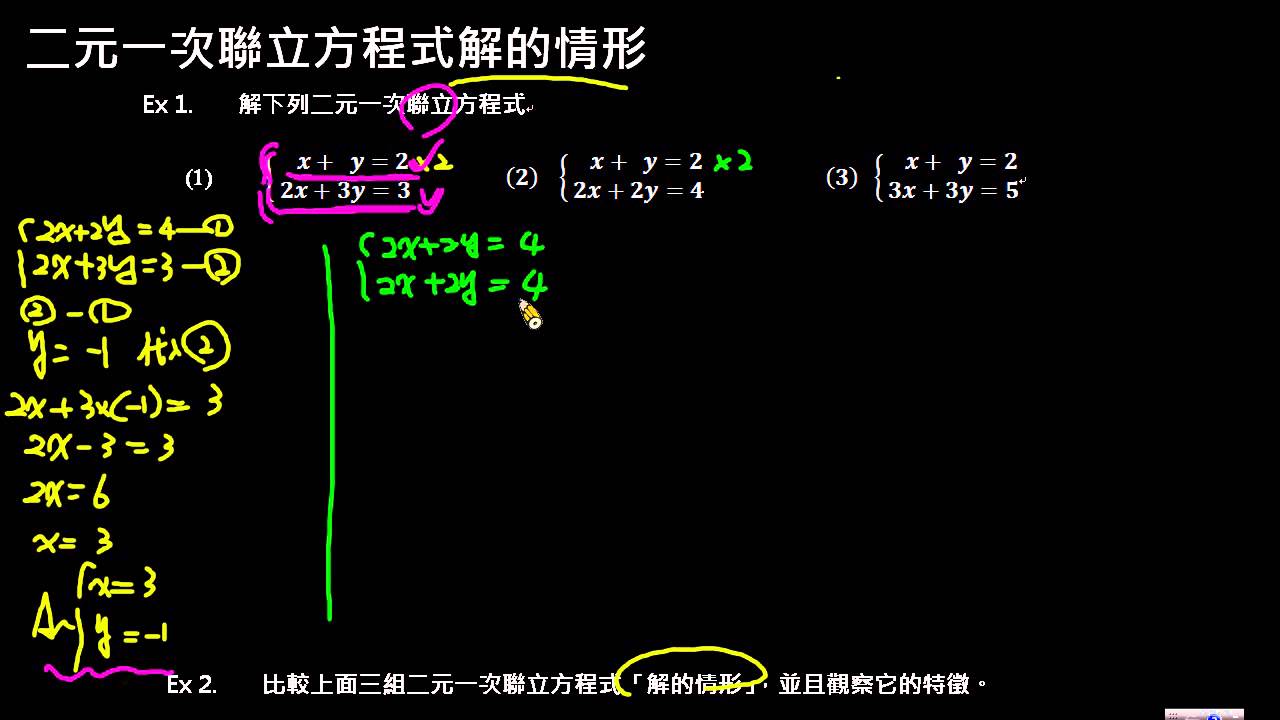



二元一次聯立方程式解的情形1 Youtube




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download
まず次の連立方程式を解いてみましょう。これは、二元連立一次方程式です。変数(未知 数)がx とy の二つだからです。右の列に書いたものは、方程式の係数だけを取り出し て書いたものです。 と= は省いてありますが、−3 のところは、(−3) と考えて−3Excelを用いた連立方程式の解法 このページでは,Excel関数を使って連立方程式を解く手順について解説する. 手順 連立方程式を行列で表現し,行列Aと行列Cの係数をExcelシートに入力する.2 3元連立1 次方程式 x,y,z を未知数とする次の連立方程式 を行列を使って次のように表すことができる。 (2) 式(2)のa, b, c, d, e, f, g, h, iを要素とした行列の行列式(determinant)をD とすると, となる。この行列式の値を求める方法は次のとおりである。




44 一次聯立方程式與矩陣的列運算 Youtube




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download
連立方程式の例 2元1次連立方程式(以下の文章では「連立方程式」と書くことにします)は例えばこんな形で出てきます。 $$\begin{cases}2xy=4\\ 4x3y=8\end{cases}$$ この情報から、\(x\)と\(y\)の解を出せと言われるのがよくあるパターンです。1 変数を方程式の逆の辺に移項します。 この「代入法」は、一つの式で「xを解く」(または他の変数を解く)ことから始まります。 例として、 4x 2y = 8 と 5x 3y = 9 という方程式があるとします。 まず最初の方程式だけを見ます。 両辺から2yを引いて式を変形させると、 4x = 8 2y となります。 この方法ではよく分数を使います。 分数が苦手な場合は、代わりにExcel の行列計算による連立方程式の解き方 消去法との比較 例題 次の連立方程式を解きます。 解説 この方程式は、行列を使って、以下のように書けます。 ここで、 とおくと、方程式の解、x、y、z は、Aの逆行列を用いて のように、求められます。




隨筆誌 二下2 3三元一次聯立方程式比例式解題想法




高二高中數學的 數甲 B4 2 3 三元一次聯立方程式筆記 Clear
連立方程式を行列を使って解くことを考えましょう。最初は、未知数が2個の場合 を考えます。以下に、連立方程式を示しました。 上の行列方程式を解いてみます。まず、左から両辺に逆行列をかけます。 ここで、逆行列は以下のように計算されます。これから連立方程式を解く問題はこの行列の形で出題されますので、元の連立方程式がどういう形なのか分かるようにしておいてくださいね! 連立方程式の解は3パターンある 連立方程式の解の出方は以下の3パターンです。 ・「 普通に解が出るパターン 」




加減消去法解二元一次聯立方程式 Youtube




1 兩個同時成立且並列在一起的二元一次方程式 稱為二元一次聯立方程式 Ppt Download



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf




B4 3 1 一次聯立方程式與矩陣 Youtube




1 3 2 1 4 2 2 15r



課業輔導中心 2 3 三元一次聯立方程組p 85




建宏國中e把罩數學 3 二元一次聯立方程式



Q Tbn And9gcr6cto4p7dzcq6zf K9artmgeytohwxvgynmlrwpcdi2wifi1eg Usqp Cau



克拉瑪公式解三元一次方程組 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌




二元一次方程组 全章复习与巩固 基础 知识讲解



1




克拉瑪公式3元一次聯立方程式請問這個敘述是正確的嗎 Clear



6 3 聯立方程式聯立方程式求行列式6 8 2 15 5 3 4 1 之值 求行列式15 10 15 15 0 6 2 6 4




國中數學2 1 2解二元一次聯立方程式




数学不好的人所欠缺的解题基本功 图表与联立方程式之间的联系 网易订阅



測評網 國一下 數學第一次段考 複習錦囊




Ppt Chapter 1 矩陣powerpoint Presentation Free Download Id




翻轉學習影片 高中 數學 三元一次聯立方程組 演練1




數學3分鐘 43 解聯立方程 Mclinhk Youtube



三元一次方程式excel 40 三元一次聯立方程式的公式解 克拉瑪公式的說明 Mtlpe



聯立方程 教育多媒體




第1章二元一次聯立方程式1 1 代入消去法一 章節內容 Ppt Download




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




三元一次聯立方程式 利用克拉瑪公式判斷三平面關係之一 Youtube



三元一次方程式求連比 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌



名師課輔網 聯立方程式的解




Ok423 三元一次連立方程組1 Ok423 三元一次聯立方程式主題一解聯立方程式1 可用加減消去法或代入消去法求解 2 聯立方程式的解可分成三種 1 恰有一解 2 無限多組解 3 無解 Pdf 免费下载




Matlab方程式求解 Ytffhew的博客 程序员宅基地 Matlab方程式求解 程序员宅基地




翻轉學習影片 高中 數學 三元一次聯立方程組 練習3




用行列式直接写出联立方程的解 云上小悟




4d F736f F Db2cb3e6a4b8a454a4b8a440a6b8c170a5dfa4e8b57bb2d52e646f63 Pdf 免费下载



2



Http Www Topmath Org J Student Pdf



三元一次聯立方程組的解 空間中三平面的關係 中學數學課 隨意窩xuite日誌




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




Chapter 1 矩陣1 1 聯立方程式1 2 矩陣的定義1 3 矩陣的運算1 4 基本列運算1 5 反矩陣1 6 行列式 Ppt Download




二元一次聯立方程式的基礎概念 均一教育平台
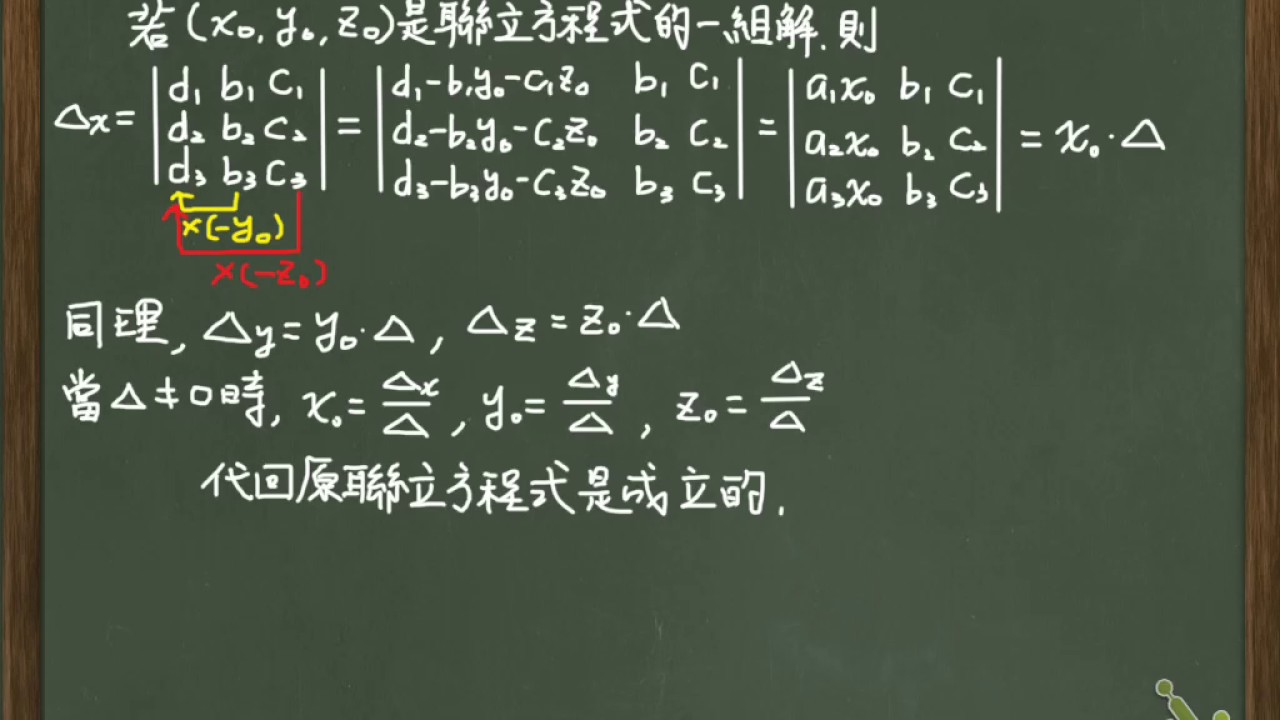



40 三元一次聯立方程式的公式解 克拉瑪公式的說明 Youtube
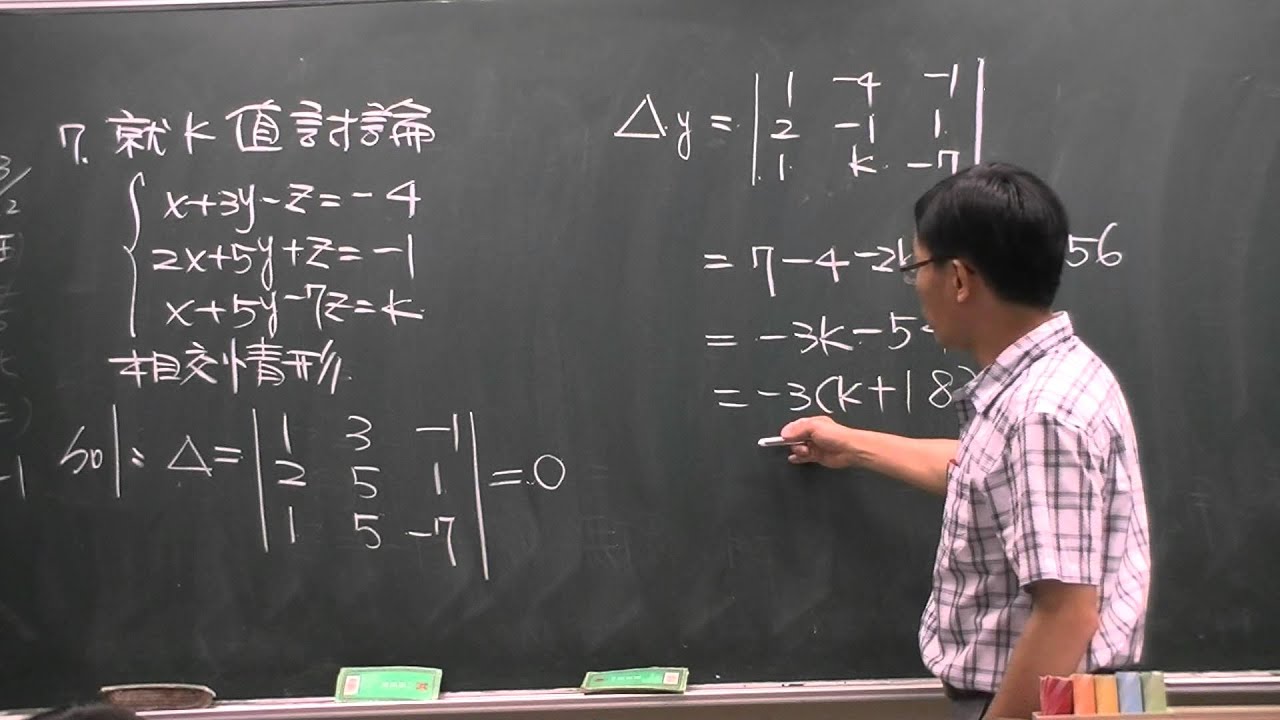



三元一次聯立方程式 由未知數討論方程組的解 Youtube



1
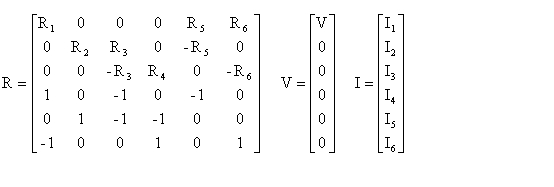



Matlab方程式求解 Ytffhew的博客 程序员宅基地 Matlab方程式求解 程序员宅基地



三元一次聯立方程組的解 空間中三平面的關係 中學數學課 隨意窩xuite日誌




6 3 联立方程计量经济学模型的识别 Ppt 6 3 联立方程计量经济学模型的识 The Identification Problem 一 识别的概念 Course Hero



2




急 Clear




例題 二元一次聯立方程式的解 數學 均一教育平台




怎麼知道的 紅線 Clear




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




1 3例題2三元一次聯立方程式的無解 Youtube




B4 2 3 三元一次方程組的加減消去法 理論 與範例1 用加減消去法解三元一次方程組 Youtube




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア



Http Math Ymhs Tyc Edu Tw Chenjt99 Scrclass 1052 E9 Ab 98 E4 Ba 8c E9 Ab 98 E4 Ba 8c E7 Bf 92 E4 9c 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E5 8f E4 9c Pdf



大家來解謎 解二元一次聯立方程式 導入活動 環遊數界




3 小柯以代入消去法解二元一次聯立方程式 計算步驟如下 請問小柯從哪一個步驟開 阿摩線上測驗




方程組 維基百科 自由的百科全書




怎麼知道的 紅線 Clear




像上面兩個二元一次方程式x Y 70 和x 2y 115 雖然各自有解 但是當聯立在一起時 我們要找的就是同時能讓兩個方程式等號成立的x Y 值 此時的x 與y 就是這兩個方程式的一組共同解 也就是聯立方程式的解 但是 要如何求出二元一次聯立方程式的解呢 讓我們先以二




加減消去法2 Youtube



Ppt Chapter 1 矩陣powerpoint Presentation Free Download Id




大家來解謎 解二元一次聯立方程式 導入活動 環遊數界



1



高斯消去法解三元一次聯立方程式




100 Epic Best2 元1 次方程式 最高のカラーリングのアイデア




3 3克拉瑪公式




1 4例題3三元一次聯立方程式的無限多解 Youtube




三元一次聯立方程式 克拉瑪公式說明 Youtube




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




求解謝謝 Clear




使用python 解線性聯立方程組 透過numpy Pyplot 與tensorflow By Yao Jen Kuo Pyradise Medium



6 5 聯立方程式聯立方程式求三階 列式15 01 1974 7 3 4 5 2 3 之值 求三階 列式99 9 7 199 4 3 29



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf




例題 解二元一次聯立方程式 綜合應用3 解二元一次聯立方程式 均一教育平台




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




联立方程是几年级学的 西瓜视频




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download




Jpdiamukpict5lpc 三連立方程式 三連立方程式サイト




例題 加減消去法2 數學 均一教育平台



二元一次聯立方程式的解 Live 多媒體數學觀念典online




請問第 個聯立方程式裡n 造成的力矩夾角為什麼是 90 8 而不是 90 8 Clear



联立方程式 快懂百科



Http Math Ymhs Tyc Edu Tw Chenjt99 Scrclass 1052 E9 Ab 98 E4 Ba 8c E9 Ab 98 E4 Ba 8c E7 Bf 92 E9 A1 8c 2 3 E7 Bf 92 E9 A1 8c Pdf




研發養成所 Bridan S Blog 4rdp For R D Person 高斯消去法 Gaussian Elimination 聯立方程式及反矩陣求解



三元一次聯立方程式 解三元一次方程組 Youtube



Http Blog Ncue Edu Tw Sys Lib Read Attach Php Id




Ch2 空間中的平面與直線2 3 三元一次聯立方程式製作老師 趙益男 基隆女中教師發行公司 龍騰文化事業股份有限公司 Ppt Download



Http Math1 Ck Tp Edu Tw E6 9e 97 E4 Bf A1 E5 Ae E5 Ad B8 E8 A1 93 E7 A0 94 E7 B6 E4 B8 8a E8 B2 E8 Ac 9b E7 Be 99 E8 B2 E7 B6 B1 E7 Ac Ac E5 9b 9b E5 86 8a 2 3 E4 B8 E5 85 E4 B8 80 E6 Ac A1 E8 81 Af E7 Ab 8b E6 96 B9 E7 A8 8b E7 B5 84 16 Pdf



0 件のコメント:
コメントを投稿