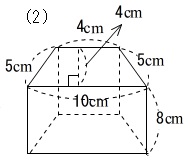
①球の体積の公式の求め方 球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r四角柱の体積 次の四角柱の体積を求めなさい。 四角柱の体積=底面積 高さ 四角柱の体積は底面積を求めて、高さを掛けるだけで完成です! まずは底面積を求めましょう。 ここで底面である四角形の面積を求めることになるので、ちょっと公式を確認 よかったら参考にしてみて。 台形の体積(正四角錐台)の求め方の公式! ? 正四角錐台の下の1辺がa、上の辺がb、高さをhとしよう。 体積は、 1/3 h ( a^2 ab b^2) で計算できちゃうんだ。 つまり、
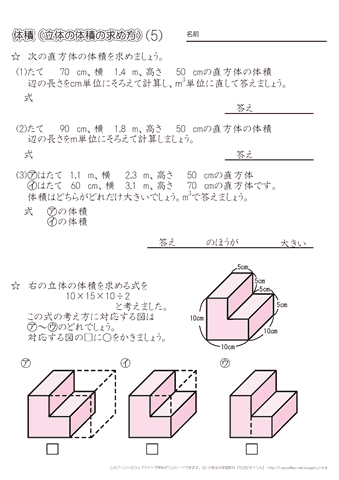
小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
体積の求め方 公式
体積の求め方 公式-V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式 jin 球の体積の求め方には公式があるんだ。 球の半径をrとすると、体積の求め方は、 $$\frac{4}{3}πr^3$$ になるよ。 つまり、 3分の4 × 円周率 × 半径 × 半径 × 半径 ってことだね。 この公式でどんなボールの体積も計算できちゃうんだ。




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
よって公式通りの結果になりました。 では最後に楕円の体積を求めてみましょう。 これは楕円の面積を求めた方法と手順は同じで、もう既に手法は紹介し尽くしているので結構簡単に結果を導くことができます。 楕円体の体積 楕円体体積の求め方 そもそも、体積の求め方は、どうやるのか? 小学校で体積を求める方法を習う立体は、立方体と直方体とそれらを組み合わせた立体です。 それぞれの体積の求め方を調べてみると、 直方体:縦×横×高さ 立方体:1辺×1辺×1辺 と書いています。 球の体積の求め方 半径rの球の体積を求める公式は、次のようになります。 πは円周率(=)です。 球の体積は、半径rの3乗に比例していくということですね! (例題) 半径5cmの球の体積は? 公式にr=5を代入して
台形の底辺と計算(求め方)、上辺の関係 台形の底辺は、 高さ 面積 上底(または下底) が既知のとき計算できます。 三角柱、角錐の体積の求め方は下記が参考になります。立方体 直方体 断面積から体積計算 公式 求め方 高さ 底面積 自動 volume球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。
5年「体積」 氏名 ⑴ たて3㎝,横4㎝,高さ5㎝の直方体の体積は, ㎤です。 ⑵ 一辺の長さが6㎝の立方体の体積は, ㎤です。 かさのことを体積 たいせき といいます。 1辺が1㎝の立方体の体積は1㎤(1立方 りっぽう センチメートル) 四角錐の高さ=四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積=12×12=144(cm²)であることから 求める四角錐の高さ=432÷144×3=9(cm)となります。 答 頑張って計算するのはもちろん,検算を必ず行いましょう。 方法としては, 1:シンプソンが使えるときはシンプソンで検算。 2:実際に図形の概形を書いてみて,目視で大雑把のに面積や体積を見積もる。 それを出てきた答えと比較して大幅にずれていないか確認。 3:単純に自分の積分計算を見直す。 他にも何か使える求積テクニックをご存じの方はご一報




円すい 円錐 の体積の求め方と問題 小学数学 Irohabook




円錐の体積ってなんであの公式なの Webty Staff Blog
円柱の体積の求め方=半径×半径×円周率×高さ 円柱に関して、体積を求める問題がよく作られます。 たとえば上の写真のように、底の円の半径と円柱の高さが示されて「この円柱の体積を求めよ」と問われます。 上の情報を元に計算の流れを説明して この公式は、これまでに説明してきた求め方にしたがうことで簡単に導くことができます。 (底面の円の面積)=(半径)×(半径)×(円周率)=r × r × π= πr 2 (円柱の体積)=(底面の円の面積)×(高さ)=πr 2 ×h= πr 2 h 円柱の体積を求めるには、与えられた半径や高さをこの公式に代入すればよいのです。 上の基本問題をこの公式を使って求める 四角錐の体積に関する問題練習はこちら⇒ 四角錐の体積の求め方 注意 円錐や角錐の体積を求めるときの公式=底面積×高さ× ですが、 をかけずに3で割っても同じです。




公式を図解 すい体の体積 円すいの表面積の求め方




立方体 直方体の体積の求め方 公式 小学生 中学生の勉強
1:球の体積の求め方(公式) まずは球の体積の求め方(公式)を紹介します。 下の図のように、 半径rの球があるとき、球の体積は4πr 3 / 3 となります。重量計算の際の体積を求めたかったため ご意見・ご感想 中空円の面積の求め方はS=π÷4((外円の直径×外円の直径)(内円の直径×内円の直径))だと思うのですが、中空円柱では÷4が無いのはなぜでしょうか? keisanより 円の直径 = 2 * 円の半径 より、数学三角錐の体積比を楽に求められる公式 ~受験の秒殺テク(2)~ キーワードは"ちぢみ率" 高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる"秒殺テクニック"を紹介していきます。




円柱の体積の求め方 公式と計算例




角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 リョースケ大学
『体積』の求め方9種類 – 公式一覧 《円・半円・弧・扇形》の円周・面積の求め方と公式一覧|小学生の算数 円に関係する公式4種類をまとめました。 重要な公式なので確実に覚えるようにしましょう。体積 = 一辺 × 一辺 × 一辺 角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので,それぞれしっかり覚えておきましょう。 ※ このQ&Aでは、 「進研ゼミ
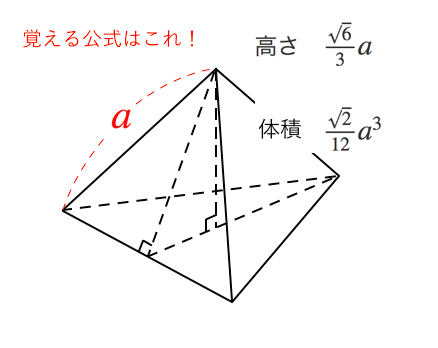



正四面体 高さ 面積を求める公式 苦手な数学を簡単に



円柱とは 体積 表面積の公式や求め方 単位あり計算問題 受験辞典
それぞれの面積はこのように計算できます。 立方体の体積: 4× 4×4=64(cm3) 4 × 4 × 4 = 64 (c m 3) 直方体の体積: 3× 4×5=60(cm3) 3 × 4 × 5 = 60 (c m 3)を使えば、 (7)式は、 S = 2∫π 2 − π 2R2cos2θdθ = 2R2∫π 2 − π 21 cos2θ 2 dθ = 2R2θ 2 1 4sin2θπ 2 − π 2 = πR2 ⋅ ⋅ ⋅ (8) S = 2 ∫ π 2 − π 2 R 2 cos 2 θ d θ = 2 R 2 ∫ π 2 − π 2 1 cos 2 θ 2 d θ = 2 R 2 θ 2 1 4 sin 2 θ π 2 − π 2 = π R 2 ⋅ ⋅ ⋅ ( 8) となります。 よって、公式通りになります。 複雑な関数や3次元の体積を求める方法の基本的な積分はこのような手法であると円錐台の体積と表面積を計算する公式と証明 具体例で学ぶ数学 > 図形 > 円錐台の体積と表面積を計算する公式と証明 最終更新日 図のような円錐台について、 体積は、 V = 1 3 π h ( a 2 a b b 2) 側面積は、 S L = π ( a b) ( a − b) 2 h 2 表面積は、 S




10 مساحت دایره Ideas In 21 Math Geometry Geometry Problems




簡単公式 3分でわかる 半球の体積の求め方 Qikeru 学びを楽しくわかりやすく
公式で出した時と同じ答えになりました。 なぜ、公式で答えを求めてみても、一辺が\(1cm\)の立方体の数を数えても、同じ答えになるのでしょうか。 直方体の体積の公式でも 直方体の体積の公式は、たて×横×高さでした。体積の求め方 立体 体積V 截頭円柱 角すい 球冠円筒 パイプ 体積計算 公式 求め方 チューブ 高さ 長さ 外径 内径 自動 volume




計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく




立方体 直方体の体積の求め方 小学生に教えるための分かりやすい解説 数学fun
Hello School 算数 体積・表面積 インターネット上で受験算数の一通りの基本的解法をマスターしよう♪。小学6年生の算数角柱や円柱の体積の求め方・公式の練習問題プリントを無料ダウンロード・印刷 (プリント5枚) 小学6年生の算数 図形の拡大と縮小拡大図と縮図 問題プリント




円柱の体積の求め方 公式 小学生 中学生の勉強




円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



3




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




丸棒の重量 円柱の体積と重量の求め方 鉄の場合
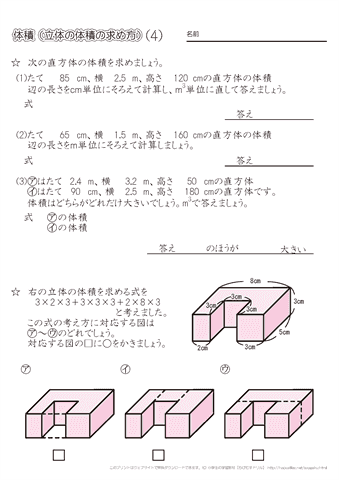



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生
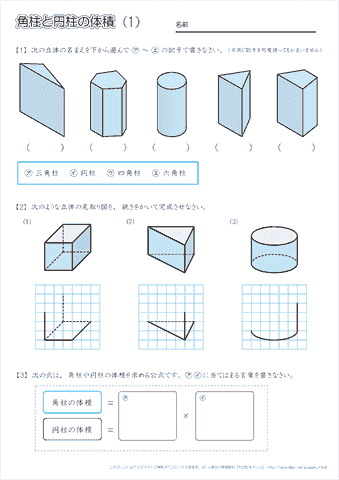



小学6年生の算数 角柱や円柱の体積の求め方 公式 問題プリント ちびむすドリル 小学生




三角柱の体積の求め方 小学生向けに問題使って解説するぞ 中学数学 理科の学習まとめサイト



立派な 台形 体積 求め 方




小5 複雑な立体の体積 直方体 日本語版 Youtube




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




計算公式 立方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




円柱の体積の公式 円の面積の求め方を覚えていないとダメ 中学や高校の数学の計算問題



球とは 体積 表面積の公式や求め方 証明 積分 と計算問題 受験辞典




円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ



5年算数体積2わかる教え方




中1数学 円柱の体積 表面積はどうやって求めるの まなビタミン




四角錐台の体積 高精度計算サイト



算数流体積の求め方 Sciencelab 冨田塾




公式を図解 すい体の体積 円すいの表面積の求め方




角柱の体積の公式 求め方は底面積と高さに注目するだけだ 中学や高校の数学の計算問題




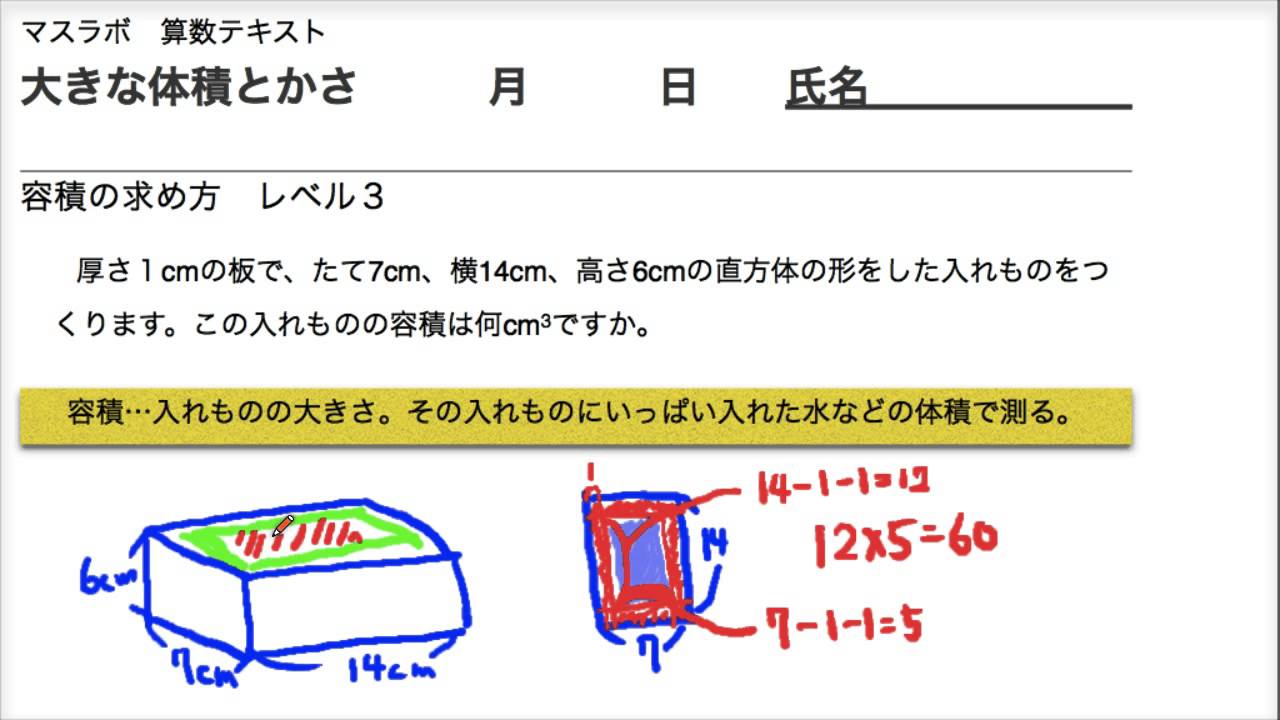
体積 容積の求め方 算数 教科質問ひろば 進研ゼミ小学講座



地図の体積計測




計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
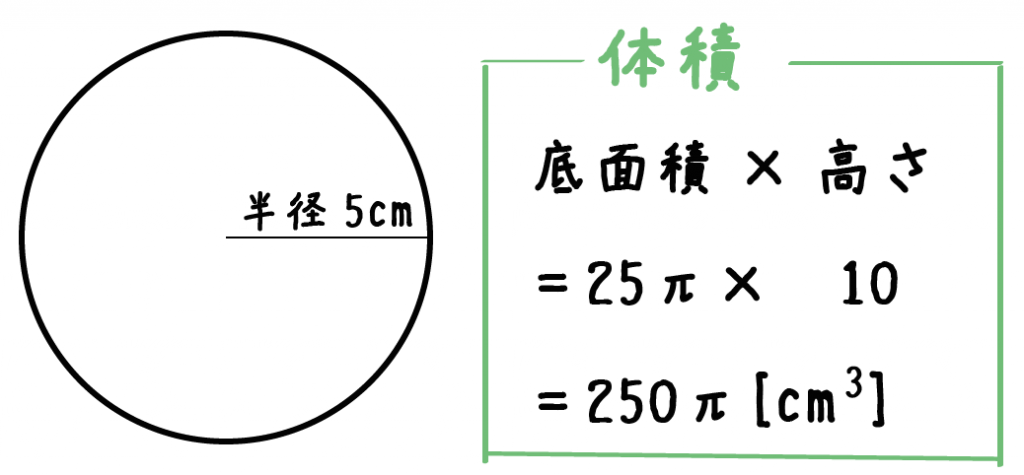



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




算数 円柱の体積の求め方 公式で確認 小学生向け 数スタ




計算公式 直方体の体積の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく




角錐 円錐の体積と表面積の公式 数学fun
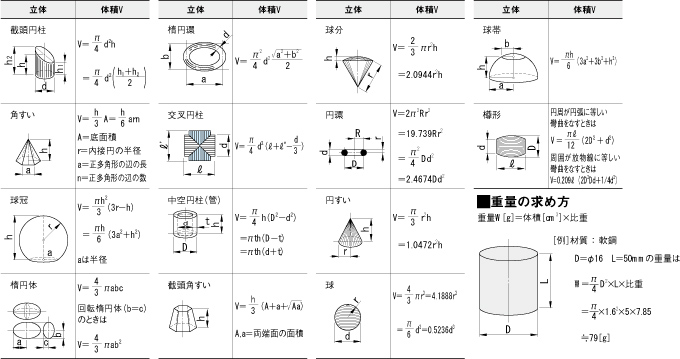



体積 重量の求め方 技術計算サイトの案内 Jis Z 02 より抜粋 ミスミ メカニカル加工部品




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット
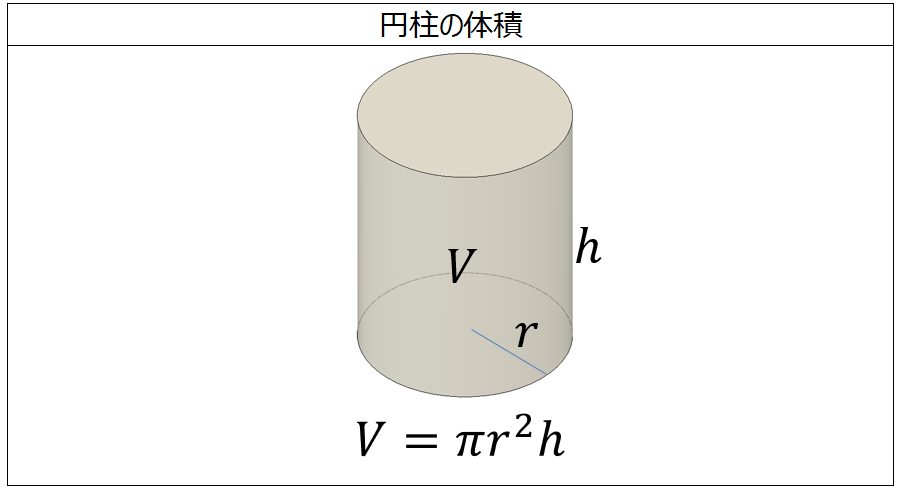



体積の計算 円柱 製品設計知識



小学校5年 算数 容積の求め方 Youtube



質量と比重




円柱の表面積と体積を求める公式 具体例で学ぶ数学




円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題




中学数学 円錐の体積の求め方 公式 サクッと なぜか分かる はかせちゃんの怪しい研究室



1




3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ




球の体積と表面積 公式と計算問題と証明 Irohabook



1



直方体 の 体積 の 求め 方 公式




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学



図形の公式一覧 図形の面積と体積はこれでバッチリ 三重の個人契約家庭教師




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




円錐の体積を求める Youtube




3分で分かる 円柱の体積 表面積の公式についてわかりやすく 合格サプリ




5年 直方体と立方体の体積 算数イメージ動画集 大日本図書



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com



Studydoctor立体の体積の求め方と公式 柱体 中学1年数学 Studydoctor




体積の求め方 計算公式一覧




3分でわかる 円錐の体積 表面積の求め方 合格サプリ




台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ




小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




三角柱の体積 表面積の求め方が図で誰でも即わかる 展開図も紹介 高校生向け受験応援メディア 受験のミカタ



球の体積の求め方の公式の絶対に忘れない覚え方を教えます Studyplus スタディプラス




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




中学数学 円柱の体積の求め方と公式 塔をモチーフ なぜか分かる はかせちゃんの怪しい研究室
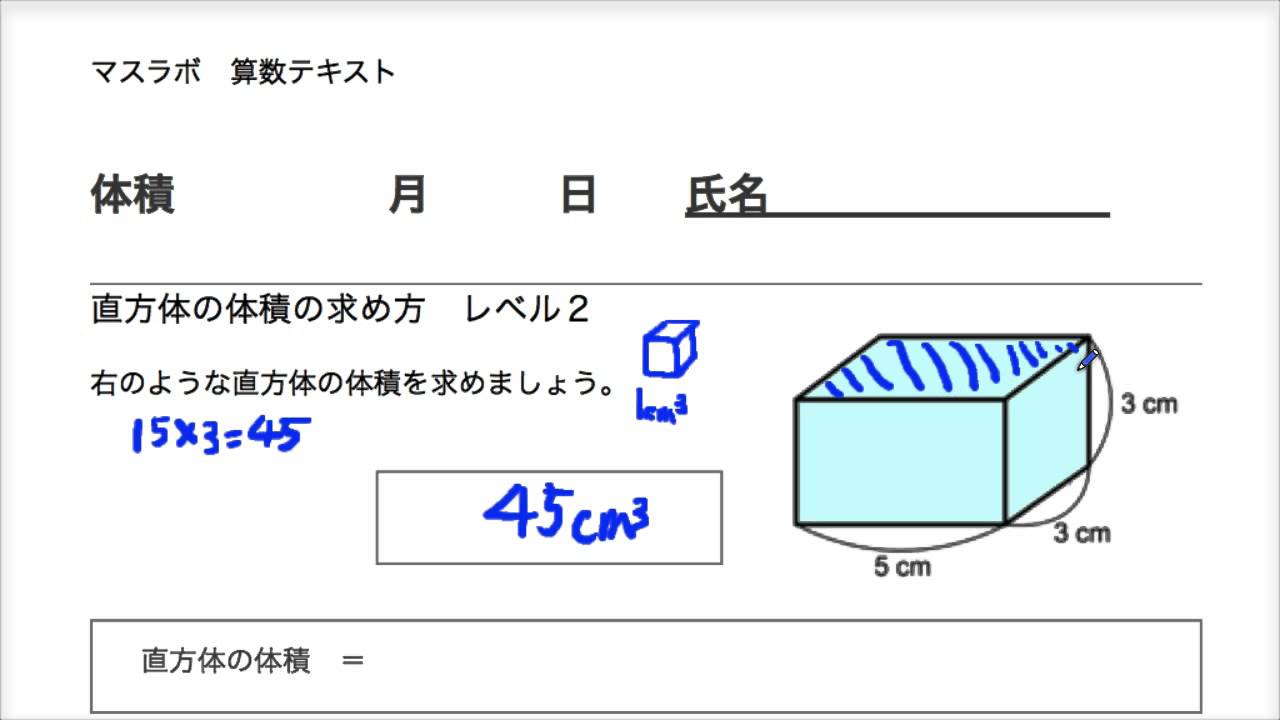



マスラボ 小学校5年 体積 レベル2 直方体の体積の求め方 Youtube




四角錐の体積の求め方 公式 小学生 中学生の勉強




体積の求め方 計算公式一覧




三角柱 四角柱 円柱の体積の求め方 具体例で学ぶ数学




体積の求め方 公式一覧 小学生 中学生の勉強




1つずつ丁寧に計算すれば解ける 円柱 の体積 表面積の求め方 お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット




中学数学 円錐の高さの求め方 頻出パターン なぜか分かる はかせちゃんの怪しい研究室



円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




円柱 の 求め 方 円柱の体積の求め方 公式 Amp Petmd Com




計算公式 正四角錐の体積の求め方がわかる3ステップ マイ勉 0で使える中学生の無料学習サイト 学習 体積 勉強法



1



6年算数立体の体積その2 教え方
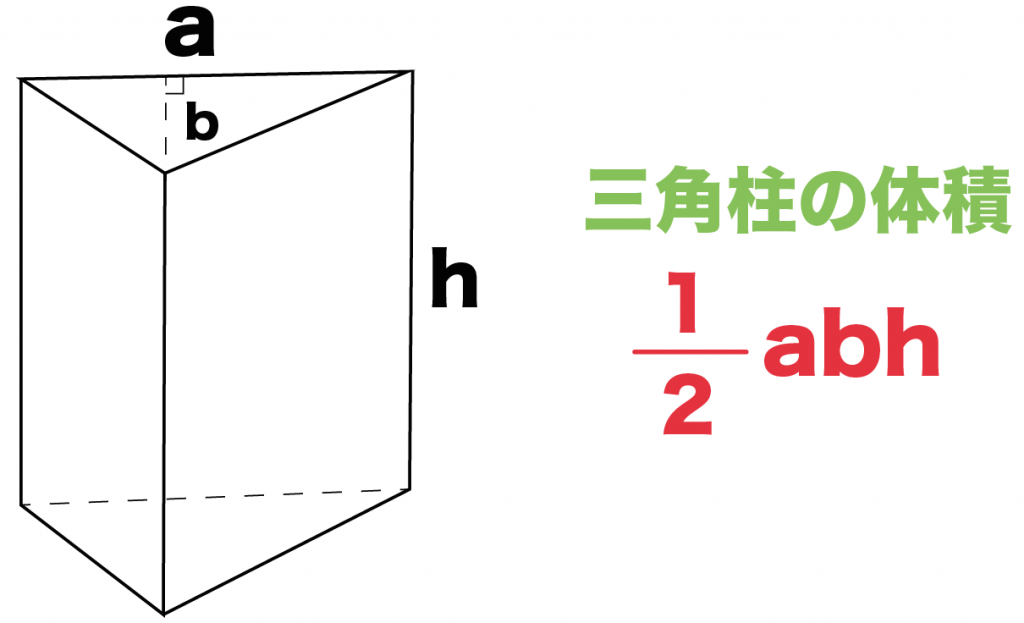



計算公式 三角柱の体積の求め方がわかる2つのステップ Qikeru 学びを楽しくわかりやすく



円錐 体積 求め 方 公式を図解 すい体の体積 円すいの表面積の求め方 Amp Petmd Com




体積の測定 測定のことを 即 知りたい ソクシリ キーエンス




計算公式 円錐の体積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




3分でなるほど 三角柱の体積 表面積の求め方をマスターしよう 数スタ




立方体の表面積と体積を求める公式と計算問題 単位との関係も ウルトラフリーダム




中1数学 円柱 円すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット




中1数学 三角柱 四角柱の体積の求め方がサクッとわかる 映像授業のtry It トライイット
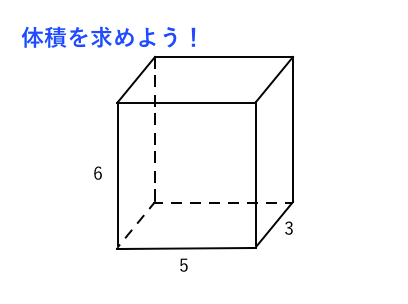



超簡単 体積の求め方 苦手な数学を簡単に




体積の求め方 計算公式一覧




小5 算数 小5 5 体積の求め方のくふう Youtube




2 を途中式を含めて教えてください Clear




3分でなるほど 四角柱の体積 表面積の求め方をマスターしよう 数スタ




6年算数立体の体積1 教え方




体積 複雑な形の立体 算数 教科質問ひろば 進研ゼミ小学講座
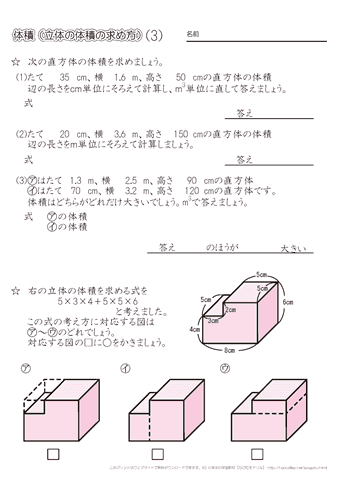



小学5年生の算数 体積 立体の体積の求め方 練習プリント ちびむすドリル 小学生




小5 算数 小5 3 直方体と立方体の体積 Youtube




体積の求め方 計算公式一覧
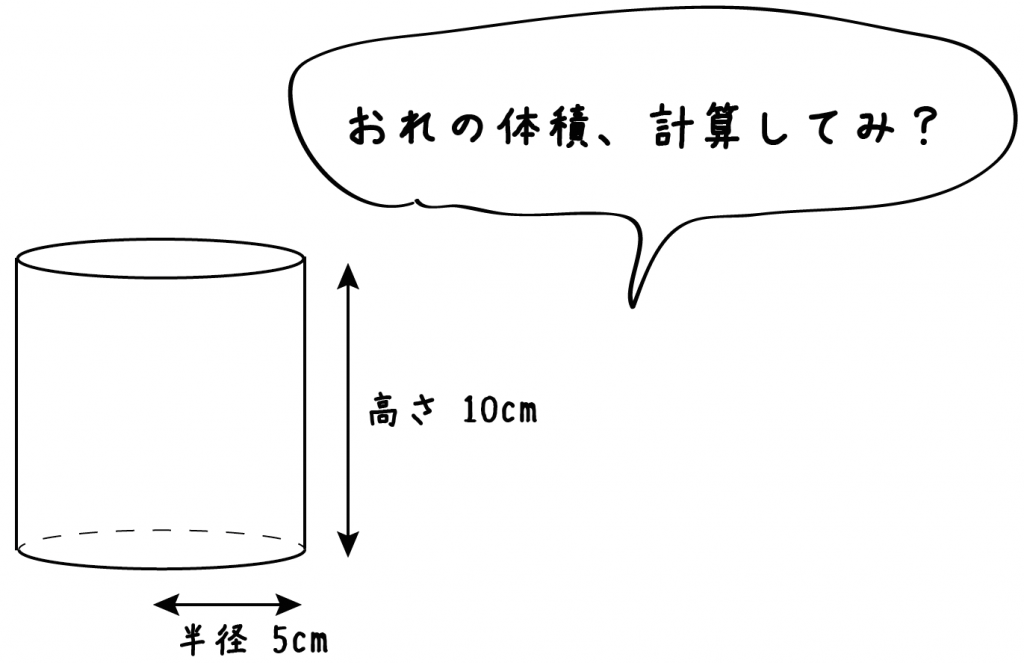



計算公式 円柱の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ




円柱の表面積と体積を求める公式 具体例で学ぶ数学



0 件のコメント:
コメントを投稿