The first position can be filled with 1 or 2 or 3, therefore there are three different ways to fill the first one The second and the third position can be filled with three different ways, tooDomain and Range Exercises STUDYSmarter Question 1 Find the domain and range of each of the following, where y is a function of x (a) y = 5x 3 Get an answer for '`y=(x4)/(x3)` Graph the function State the domain and range' and find homework help for other Math questions at eNotes
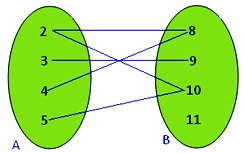
Domain And Range Of A Relation Worked Out Problems On Domain And Range Range
Domain and range of y 4 3 x
Domain and range of y 4 3 x-How to Find the Domain and Range of f(x, y) = ln(xy 2)If you enjoyed this video please consider liking, sharing, and subscribingYou can also help supportStep 3 Finally, the domain and range will be displayed in the new window What is Meant by Domain and Range?




Find The Domain And The Range Of The Real Function F X X 3 X 5
FInd domain and range `R={(x,y);x` is an integer and `x lt 3 and y=x3}`Domain and Range The domain of a function is the set of values that we are allowed to plug into our function This set is the x values in a function such as f(x) The range of a function is the set of values that the function assumes This set is the values that the function shoots out after we plug an x value in They are the y values In this case, the range of the function starts at y=x36 As the range starts at 6, precisely the point (0,6) no matter which value you pick for x As the function continues with no restriction and goes on and on we can say the Range belongs to this interval 6, ∞) or {y ∈ R /y≥6}
Range all the values that y will be after we put all the domain values ( some time it could be a bit tricky ) One way to find the Range is to Solve for x ( find the inverse ) y (x3) = 2 → yx 3y = 2 → yx = 23y → x = (23y)/y So, y can not be 0 that means the Range is all real numbers Except ySubstitute 1 into the quadratic to get 1^2 2 (1) 5 = 1 2 5 = 4 Vertex is at (1,4) and it opens upward Since no values of x are negative, domain is all real numbers Then, since the vertex is the low point, take the primary square root of 4 to get 2, so range is y ≥ 2For your function, there are two obvious restrictions on the domain It can't be 0, and (x3)/x must be greater than or equal to zero The latter evalutes to 1–3/x >= 0 or 3/x = 3 Since 0 < 3 we can summarize this as the domain is all x >= 3 For the range, at 3 the value is 9 For large x the function is clearly increasing
Domain and range » Tips for entering queries Enter your queries using plain English To avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask for the domain and range domain of log(x) (x^21)/(x^21) domain;–1 x 2 4 y 021 Mathematics Learning Centre, University of Sydney 5 State its domain and range Solution The function is defined for all real xThe vertex of the function is at (1,1) and therfore the range of the function is all real y ≥ 1 12 Specifying or restricting the domain of a functionX = 3 Domain is all reals EXCEPT 3 For range, solve y= (2x7) / (x3) for x y (x 3) = 2x 7 yx 3y = 2x 7 yx 2x = 7 3y x (y 2) = 7 3y x = (7 3y) / (y 2) y cannot equal 2, since y 2 would equal zero
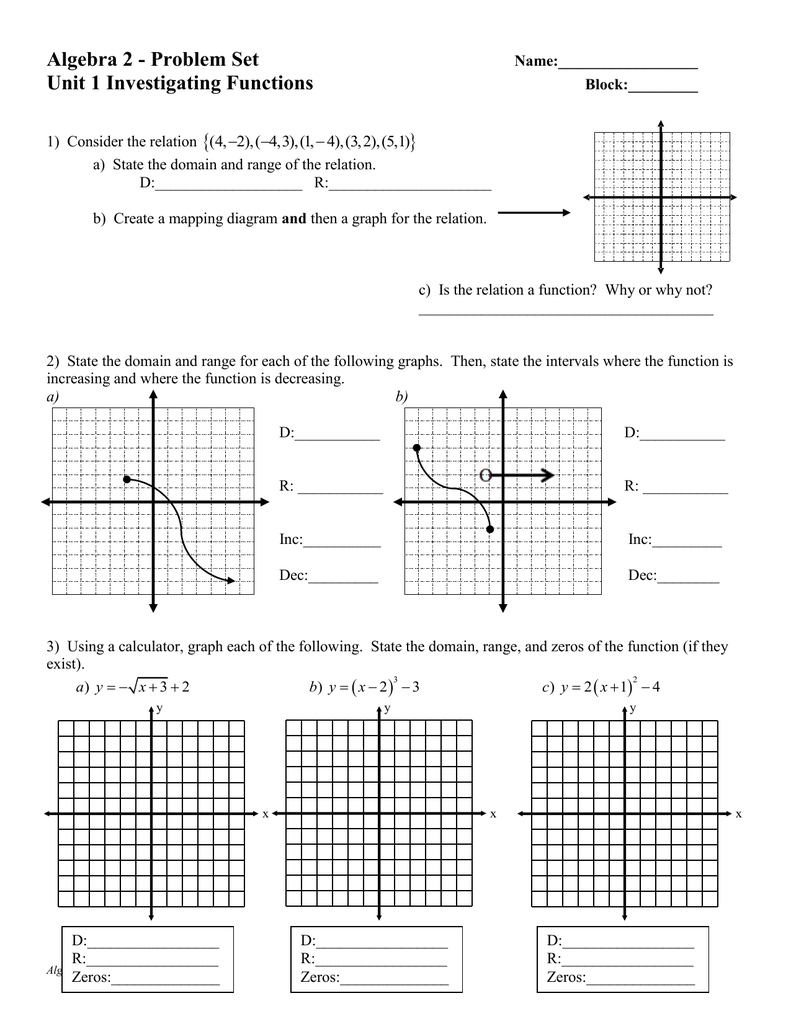



Algebra 2 Problem Set
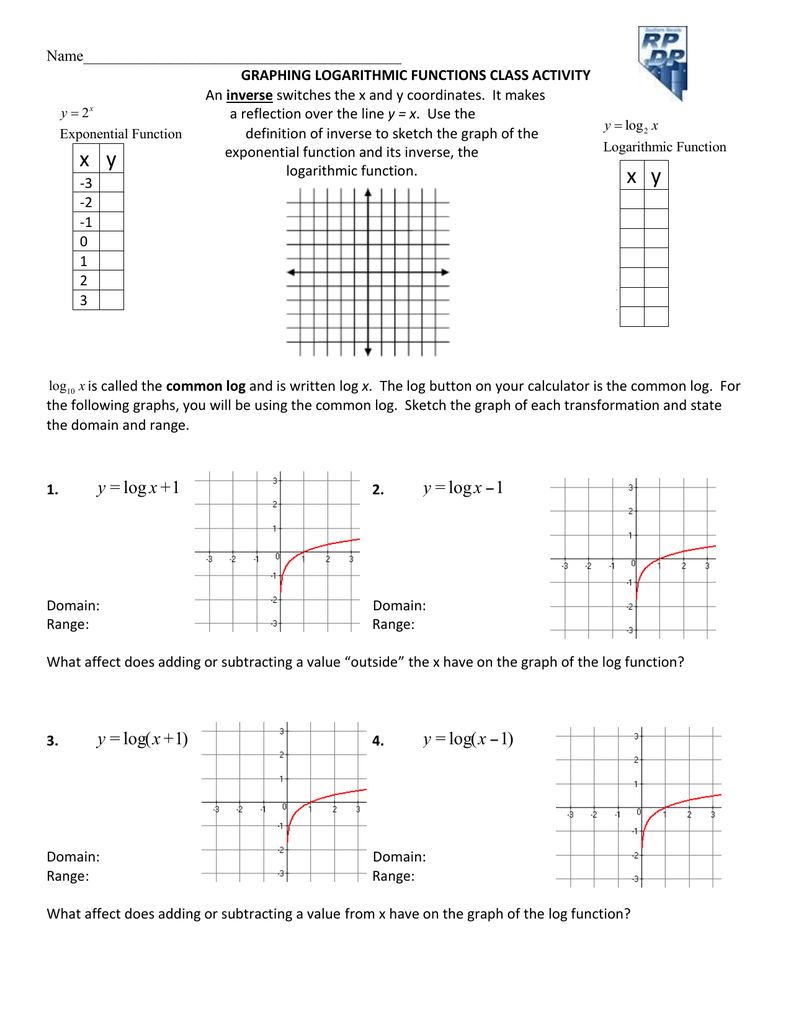



Name Inverse Y X
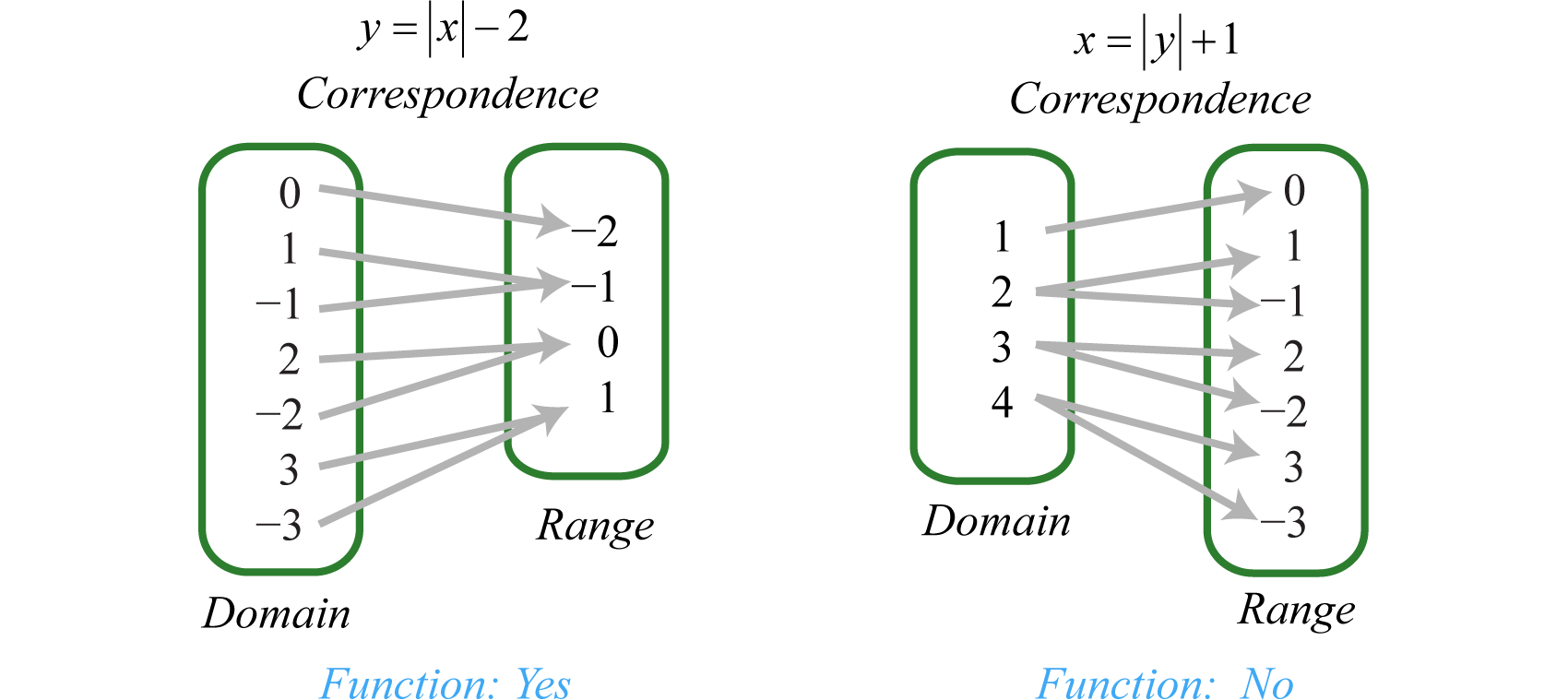
Answer The domain is all real numbers, and the range is all real numbers f ( x) such that f ( x) ≤ 4 f ( x) ≤ 4 You can check that the vertex is indeed at (1, 4) Since a quadratic function has two mirror image halves, the line of reflection has to be in the middle of two points with the same y valueClick here👆to get an answer to your question ️ Domain and range of f(x) = x 3x 3 are respectivelyEven though they are represented differently, the above are the same function, and the domain of the function is x = {2, 3, 5, 6, 8} and the range is y = {4, 8, 2, 9, 3} This is how you can defined the domain and range for discrete functions The order in which you list the values does not matter But how do you define the domain and range for functions that are not discrete?




What Is The Domain Of Y X 3 Donimain
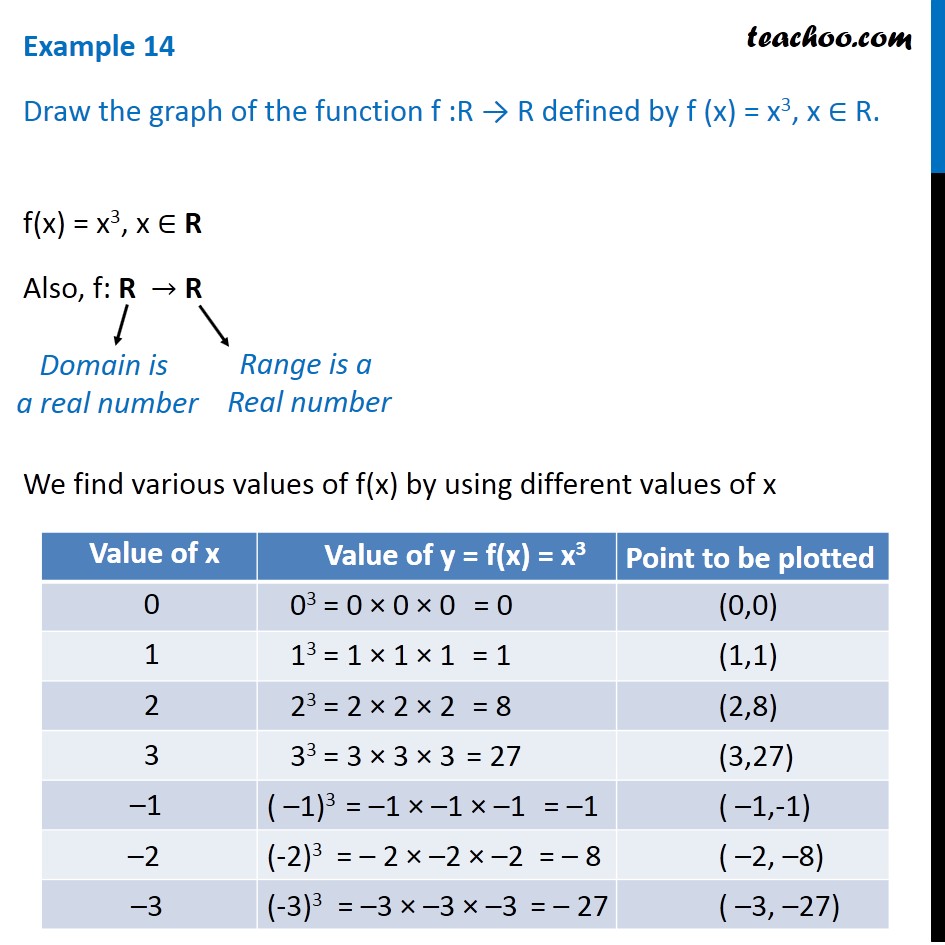



Example 14 Draw Graph Of F X X 3 Chapter 2 Class 11
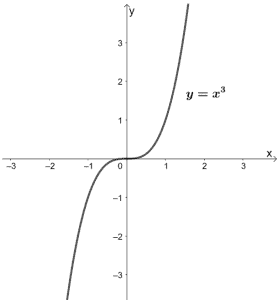
X 3 = 0 ⇒ x = − 3 So, the domain of the function is set of real numbers except − 3 The range of the function is same as the domain of the inverse function So, to find the range define the inverse of the function Interchange the x and y x = 1 y 3 − 5 Solving for y you get, Computers and Technology, 1400, seanisom7 Find the domain and range of Y=x^39/x3Solution x 3 is a polynomial, which means its domain is R, and in our case, its range is also R because the only root that x 3 has, 0, is not a double root (technically it's a triple root, and because 3 is odd, the function switches sign) Both the domain and range are all real numbers, or R




How To Find Domain And Range From A Graph Video Khan Academy
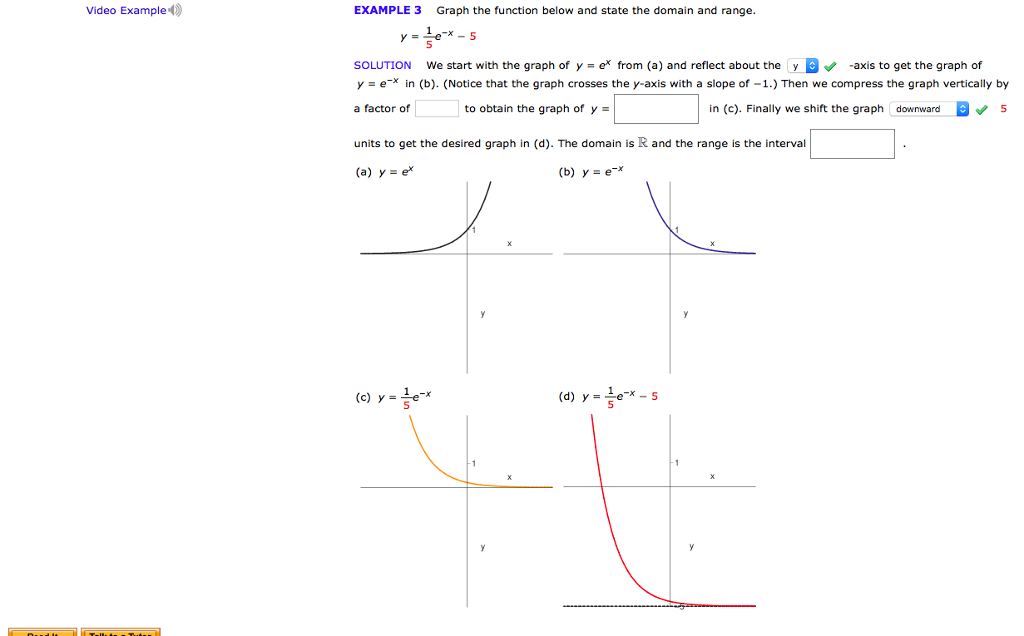



Solved Graph The Function Below And State The Domain And Chegg Com
Solution for Determine the domain and range of each of the following function 1 y=x 3 у 3х?Correct option is A {1,3},{2,1} The possible values of x which satisfies the given relation is the domain of the relation The possible values of y which satisfies the given relation is the range of the relation Given that x,y are natural numbers and the relation is x2y=5 For x=1 , the value of y is 2 For x=3 , the value of y is 1Range Let y = f(x) be a function Range is all real values of y for the given domain (real values of x) Let us look at some examples to understand how to find domain and range of a function Example 1 Find the domain and range of the following function f(x) = x / (1 x 2) Solution Domain of the function f (x) f(x) = x / (1 x 2)
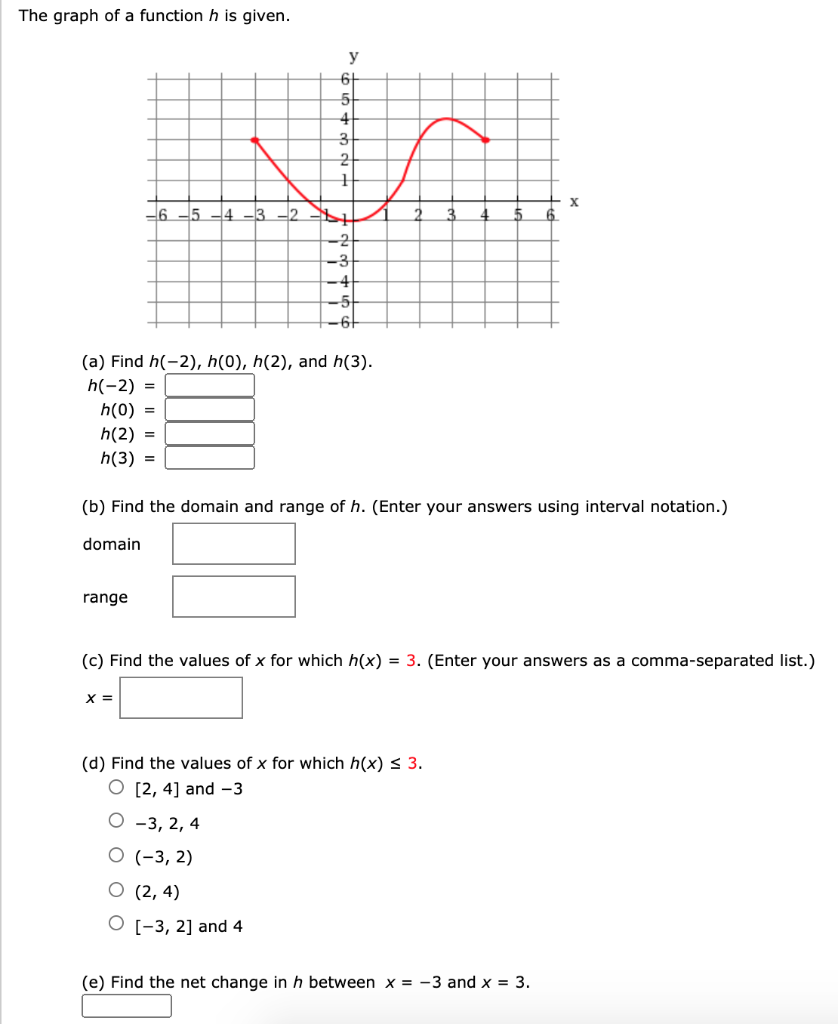



Solved The Graph Of A Function H Is Given Y 6 5 4 3 1 X 6 Chegg Com



Finding Domain And Range Activity Builder By Desmos
Finding Domain and Range from Graphs Another way to identify the domain and range of functions is by using graphs Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the xaxis The range is the set of possible output values, which are shown on the yaxis Keep in mindDomain and Range The domain of a function f ( x ) is the set of all values for which the function is defined, and the range of the function is the set of all values that f takes (In grammar school, you probably called the domain the replacement set and the range the solution set They may also have been called the input and output of the function)Algebra Find the Domain and Range y=3^x y = 3x y = 3 x The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x x
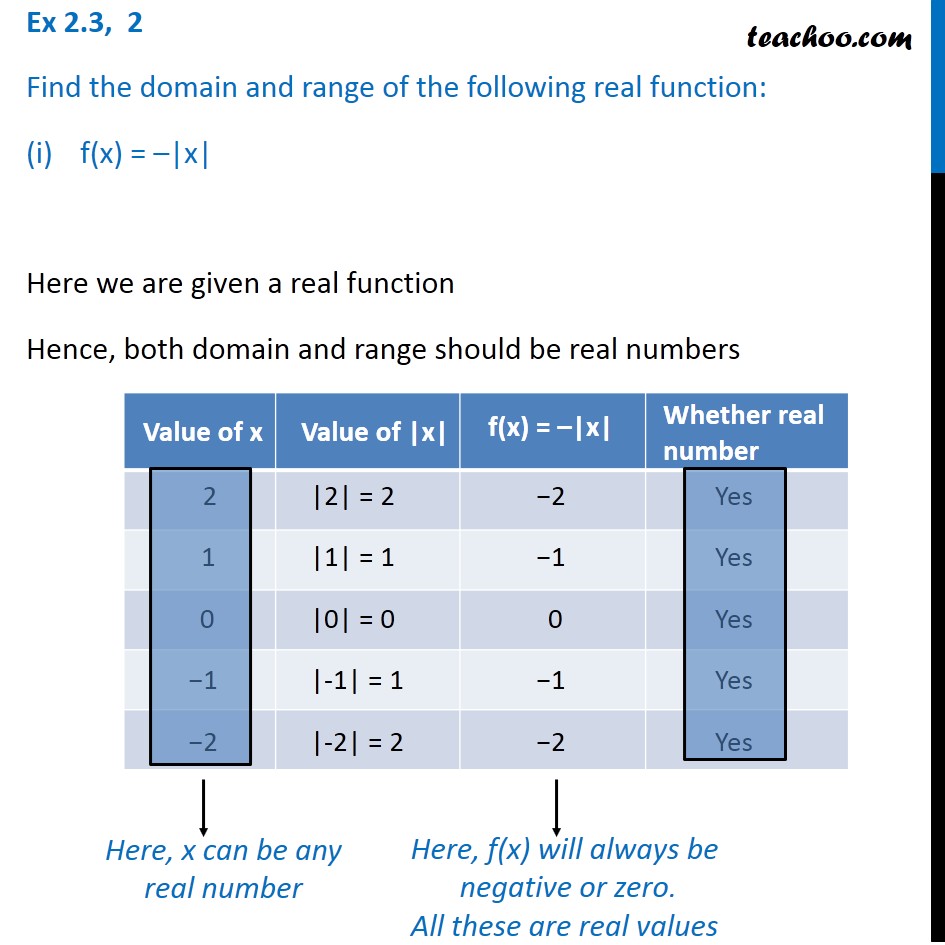



Ex 2 3 2 Find The Domain And Range Of The Function F X X
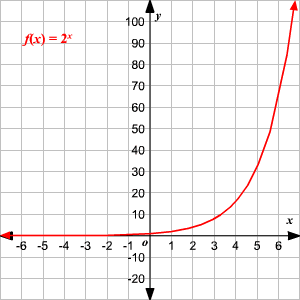



Domain And Range Of Exponential And Logarithmic Functions
Range R Period ˇ Domain, Range, and De nition of the three main inverse trigonometric functions 1 sin 1(x) Domain 1;1 Range ˇ 2;Range The set of all the outputs of a function is known as the range of the function or after substituting the domain, the entire set of all values possible as outcomes of the dependent variable For eg the range of the function F is {19, 1987, 1992, 1996} On the other hand, the whole set B is known as the codomain of the function Let's look at a simple linear function y = 4 x 3 We are going to find the domain and range using just the equation, by looking at a graph, and by looking at a table Let's think about this algebraically for a minute The domain is any number we can put in place of the x




Domain And Range Of A Relation Worked Out Problems On Domain And Range Range



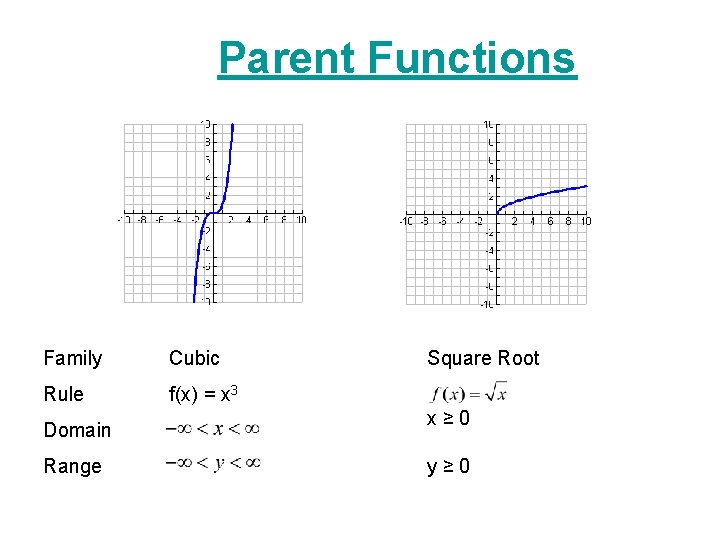
Parent Functions Types Properties Examples
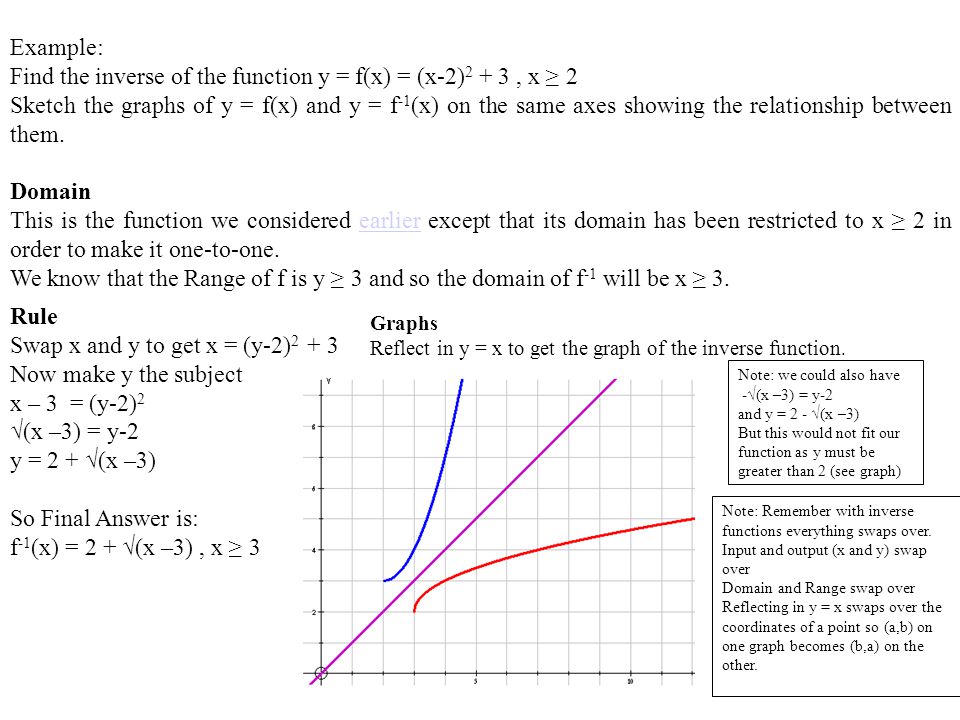
Figure 3 Domain and range of a function and its inverse When a function has no inverse function, it is possible to create a new function where that new function on a limited domain does have an inverse function For example, the inverse of f ( x) = x \displaystyle f\left (x\right)=\sqrt {x} f (xUnderstanding the translations can also help when finding the domain and range of a function Let's say your problem is to find the domain and range of the function y=2sqrt(x3) Begin with what you know You know the basic function is the sqrt(x) and you know the domain and range of the sqrt(x) are both 0,infinity)Free functions domain calculator find functions domain stepbystep This website uses cookies to ensure you get the best experience By using this website, you agree to our Cookie Policy
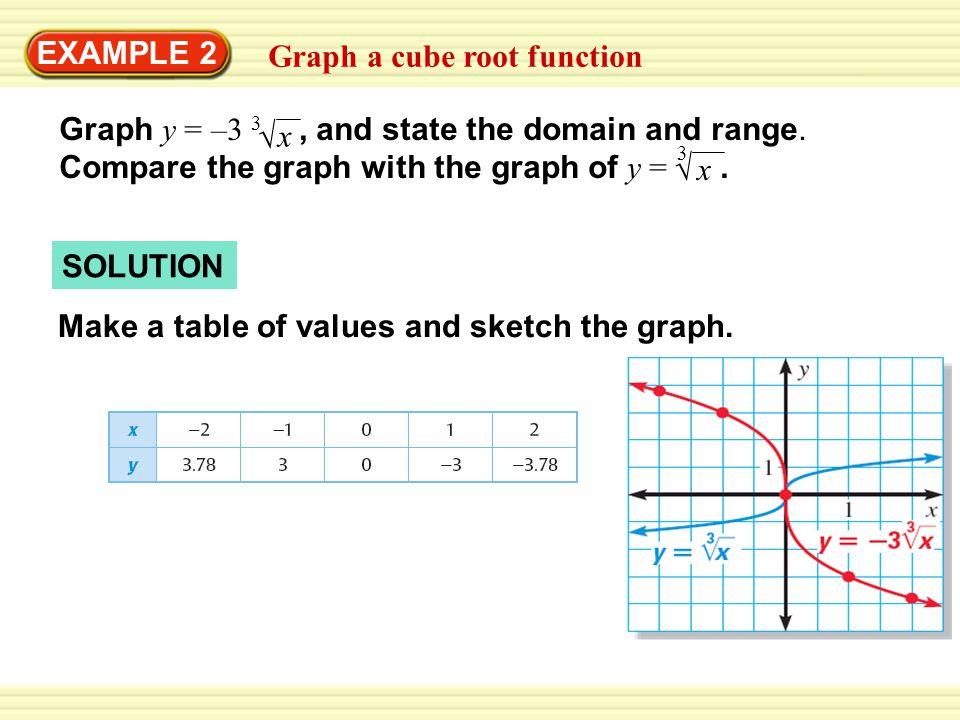



Example 1 Graph A Square Root Function Graph Y And State The Domain And Range Compare The Graph With The Graph Of Y 1 2 X X Solution Make A Table Ppt Download
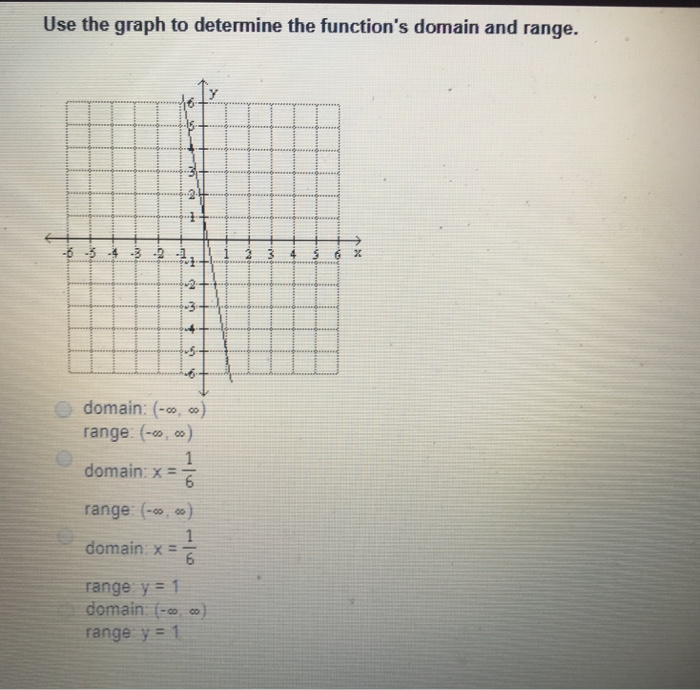



Solved Use The Graph To Determine The Function S Domain And Chegg Com
2 De nition = sin 1(x) means sin( ) = xwhen 1 x 1 and ˇ 2 ˇ 2 2 cos 1(x) Domain 1;1 Range 0;ˇ De nition = cos 1(x) means cos( ) = xwhen 1 x 1 and 0 ˇ 3 tan 1(x) Domain R Range ( ˇˇ 2;Given function is y=1x3It can be expressed as y=4x,x>=3 =x2,xIn Mathematics, a domain is defined as the set of possible values "x" of a function which will give the output value "y" It is the set of



Content Finding Domains And Ranges



Relations Graphs And Functions
Solution The given function is a logarithmic function and it has a vertical asymptote at x = −3 x = − 3 the domain of the function is (−3, ∞) ( − 3, ∞) and its range is (−∞, ∞Algebra Find the Domain and Range y=x^3 y = x3 y = x 3 The domain of the expression is all real numbers except where the expression is undefined In this case, there is no real number that makes the expression undefined Interval Notation (−∞,∞) ( ∞, ∞) Set Builder Notation {xx ∈ R} { x x The domain and range of y = 3 √x is all real numbers You can verify this by the graph of this function There is no value of x that makes the function undefined If you take the cube root of a number it can be positive, negative, or zero (the cube root of 0 is zero)



Understanding Domain And Range Part 1




Find Domain And Range Of Following Function Y X 3
Find the domain and range of the function y=3(1/5)^xThoughts (1/5)^x can get close to zero but can never be negative So domain is all Real Numbers and range is all Real numbers greater than zero ===== Cheers, Stan H The function is y = x 3 2 The value of x 3 is either positive or zero If x 3 is positive then y = positive value 2 > y > 2 If x 3 is zero then y = 0 2 > y = 2 Therefore y value start with 2 to infinity Range is y ≥ 2Create your account We are given the function y = x3 x29 y = x 3 x 2 9 We want to find the domain and range
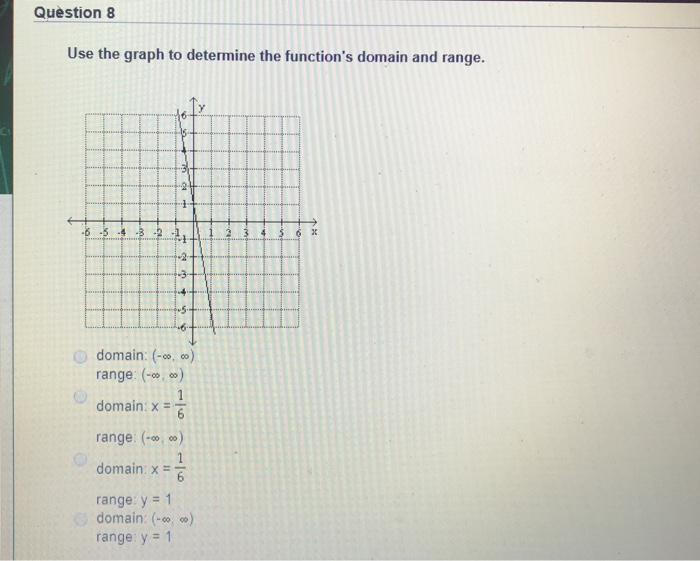



Solved Question 8 Use The Graph To Determine The Function S Chegg Com



Finding Domain And Range
Find the domain of 1/(e^(1/x)1) function domain square root of cos(x) The domain, or values for x, can be any real number, but the range does have restrictions Not all y values will appear on the graph for this equation To find the range, first find the vertex, which is located at ( h , k )Answer and Explanation 1 Become a Studycom member to unlock this answer!




Find The Domain And Range Of The Function F X 1 1 X 2 X In R X 1 Dot




Domain And Range Of Functions
4 4 y = V5 2x 2 y = VxWe are given the equation y = 2(x – 3)^2 – 4 and is asked for the domain and range of the following function In this case, there is no radical sign so the domain includes all real numbers The range has a minimum value of 4 since the squaring makes A Relation R is given by the set {(x, y)/y = x 3, x ∈ {0, 1, 2, 3, 4, 5}} Determine its domain and range



1




Answered Function Domain X Range Y Y X2 Bartleby
Domain is all real values of x = 3with a domain of x = 3, the range will be y = x3 meaning that y = 3x or y = (3x)if x = 3, then y will be 0 or 0 if x = 0, then y will be 3 or 3 if x is less than 0, then y will be a value > 3 or 3looks like the domain is x = 3, and the range is all real values of ylet's see how that works



The Domain Of F Is The Set Of All Allowable Inputs X Values Ppt Download



Domain And Range



What Is The Range Of A Function Expii




Solved Determine What Are The Domain And Range Of The Chegg Com
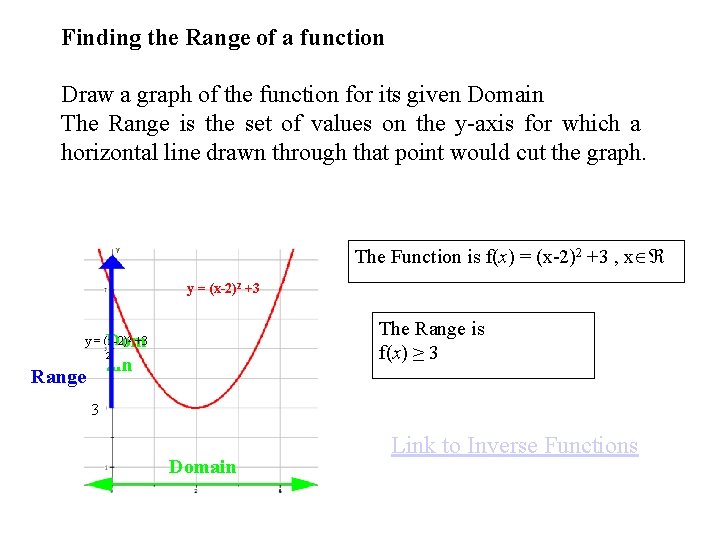



Functions Domain Range F X Y Fx A




Ppt Function Iii Powerpoint Presentation Free Download Id




Graphs Of Parent Functions Domain And Range Youtube
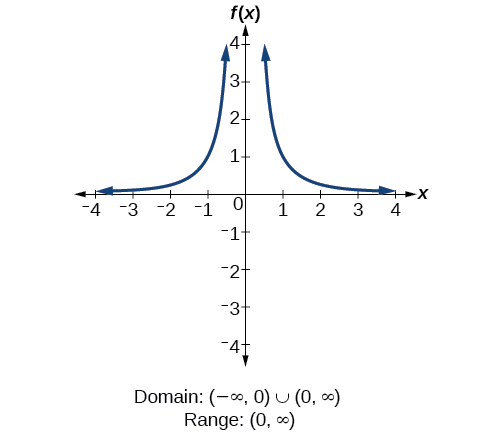



3 3 Domain And Range Mathematics Libretexts




How To Find Domain And Range Of The Inverse Of A Relation Sat Math



What Is The Domain And Range Of 1 X 3 Quora



Domain And Range Mathbitsnotebook A1 Ccss Math
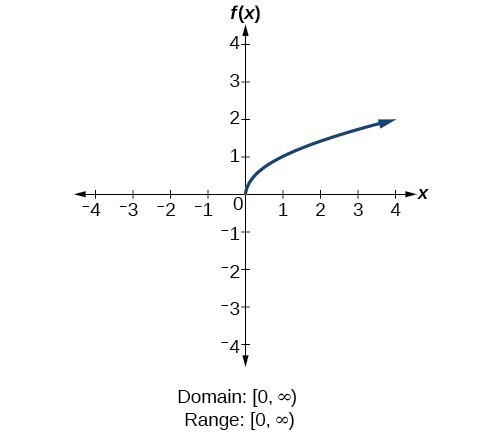



Determine Domain And Range From A Graph College Algebra



Find The Domain And Range F X 2 X 3 Displaystyle Fleft Xright 2 X 3 Snapsolve



Find Range Of Square Root Functions




Example 4 Graph A Translated Square Root Function Graph Y 2 X 3 2 Then State The Domain And Range Solution Step Graphing Quadratics Function Of Roots




Domain And Range Of Quadratic Functions Video Khan Academy




Find The Domain And Range Of The Function F X X 2 9 X 3
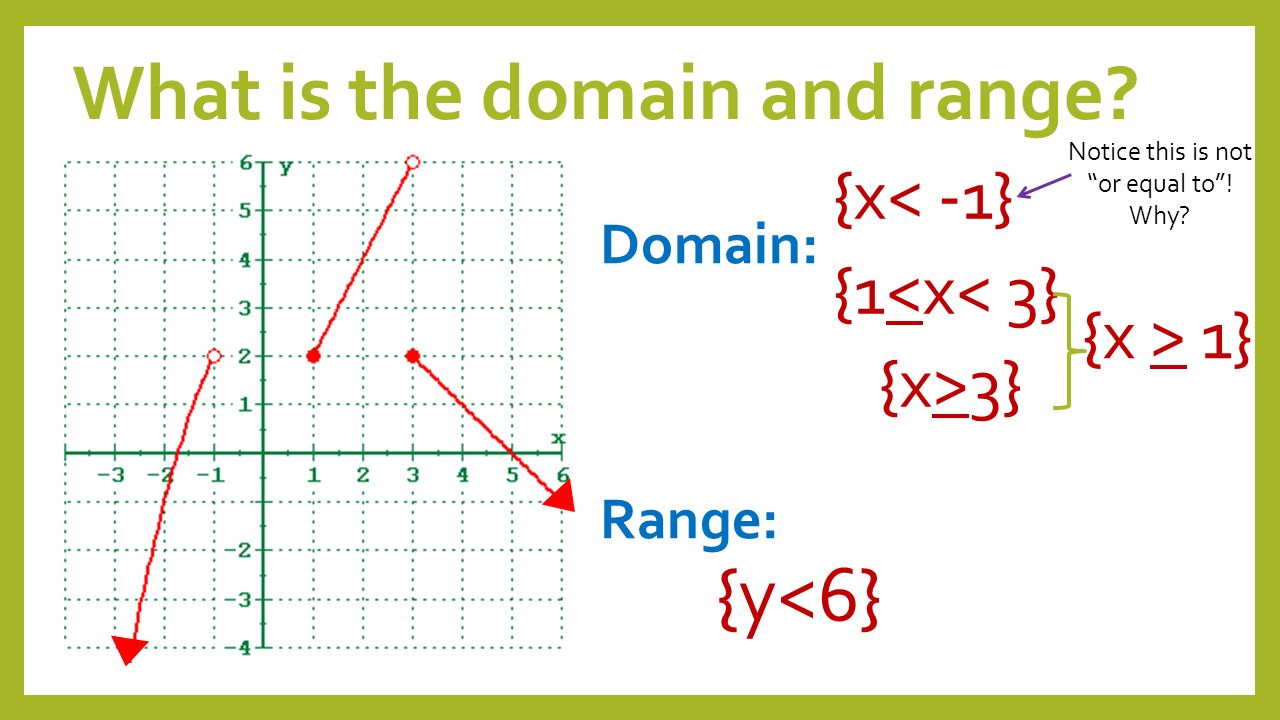



Bell Ringer Y 4 All Real Numbers Domain Range Ppt Video Online Download



Xvsmza9u3dgagm
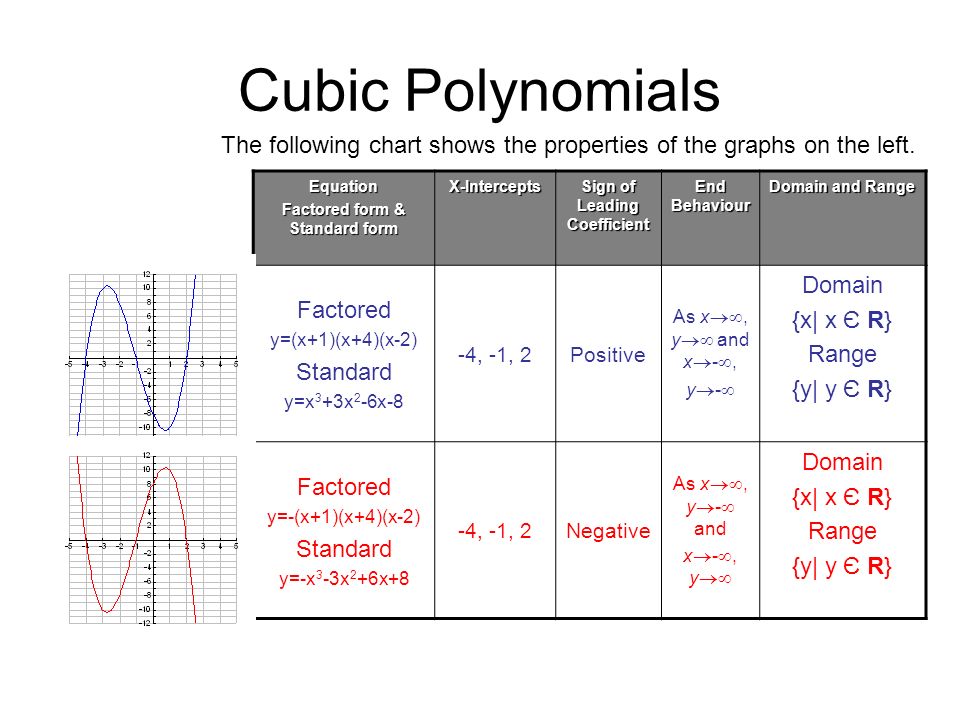



Polynomial Functions Mct4c1 Polynomial Functions The Largest Exponent Within The Polynomial Determines The Degree Of The Polynomial Polynomial Function Ppt Download
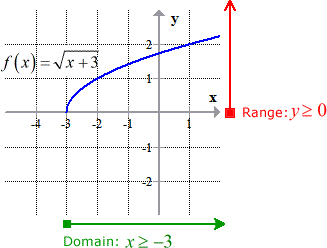



Inverse Of Square Root Function Chilimath




6 Ways To Find The Domain Of A Function Wikihow




Domain And Range Calculator With Steps Free 21



Domain And Range And Composition Of Functions



Warm Up 924 For Each Function Evaluate F0




The Domain Of A Function G X Is X Gt 3 And The Range Is Y Gt 1 What Are The Domain And Range Brainly Com



Domain Range Of Quadratics Matching By Stoked About Math Tpt
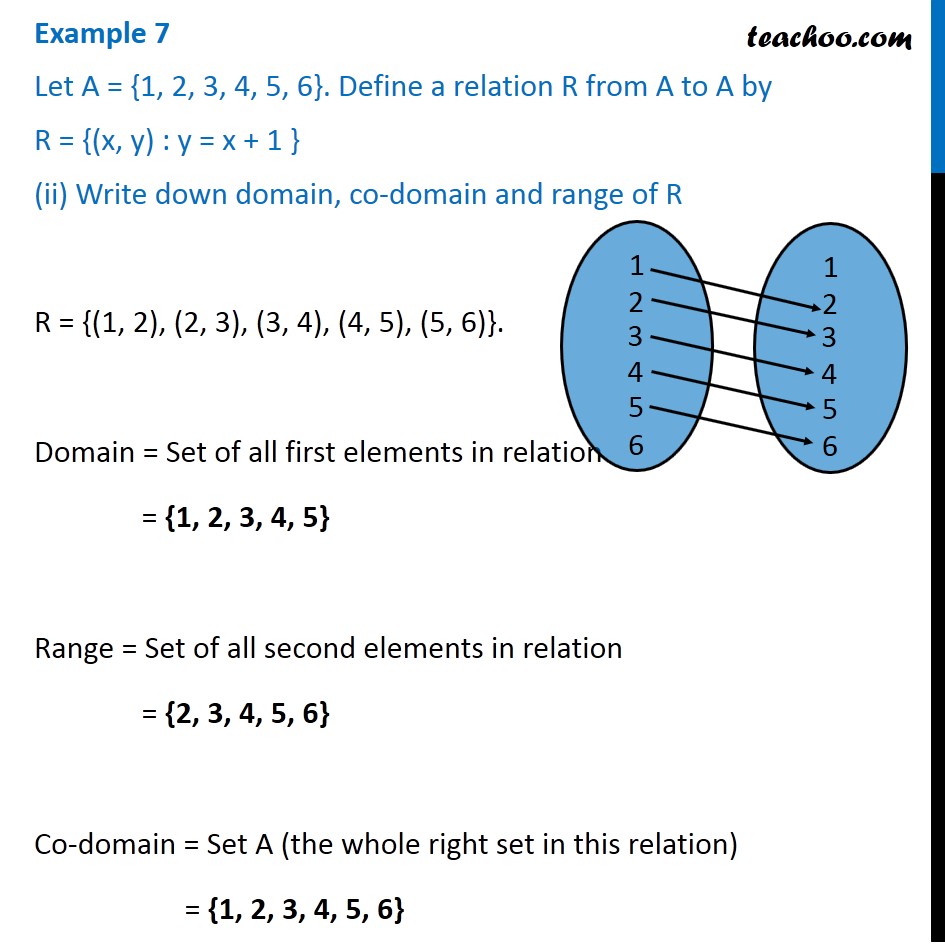



Example 7 Let A 1 2 3 4 5 6 R X Y Y X 1




Functions




Solved State The Domain And Range Of The Function Enter Your Answers Using Interval Notation Y X 3



Find The Domain And Range Of Xy X 3y 1 Mathskey Com
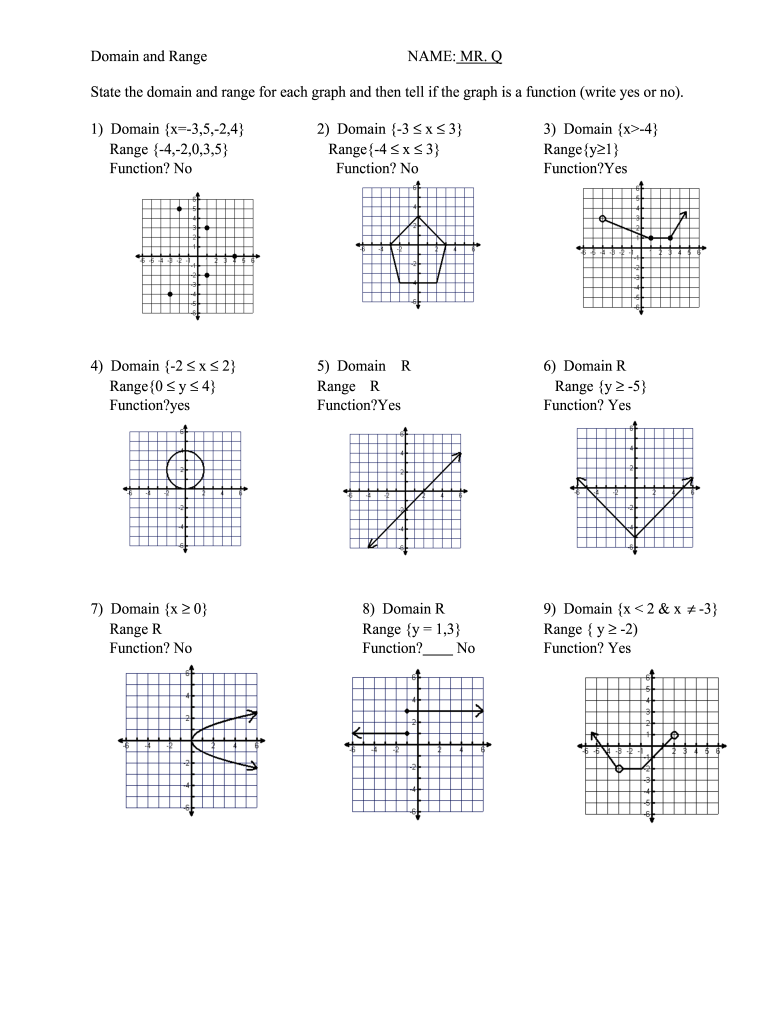



Domain Range Worksheet Fill Online Printable Fillable Blank Pdffiller




Domain And Range Free Math Help
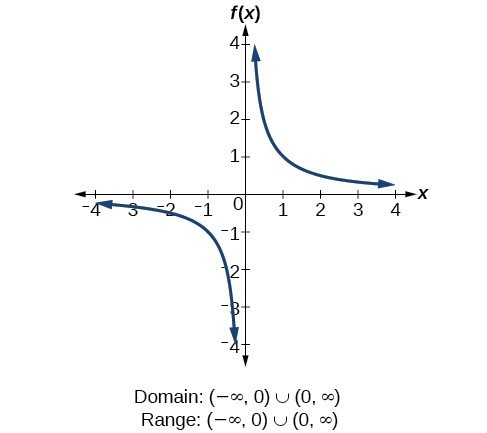



Determine Domain And Range From A Graph College Algebra
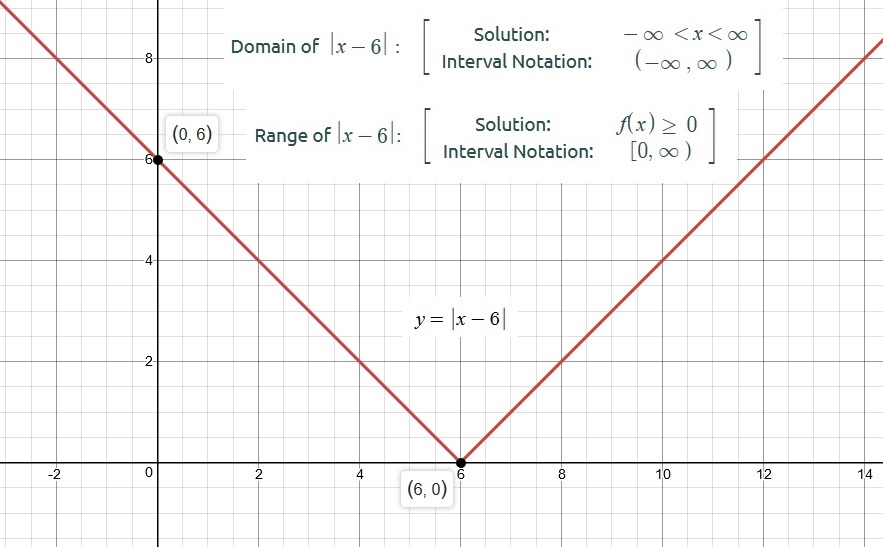



How Do You Find The Domain And Range Of Y X 6 Socratic



Graph Domain And Range Of Absolute Value Functions
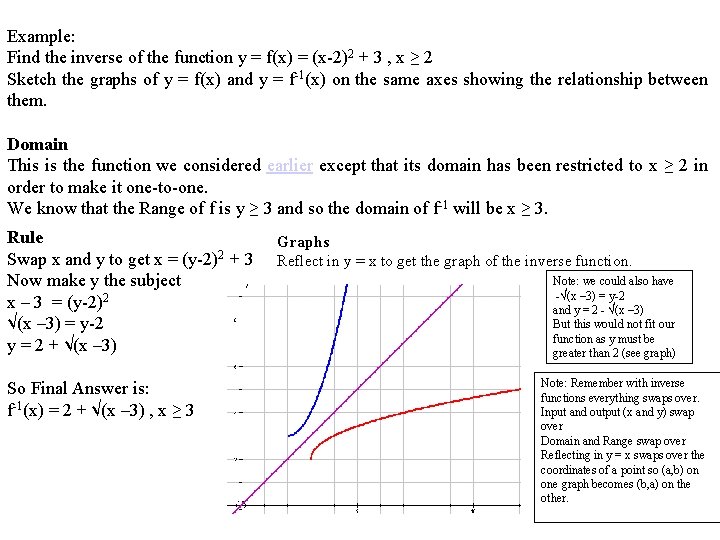



Functions Domain Range F X Y Fx A




Finding The Domain And Range Of A Function Graphically Expii
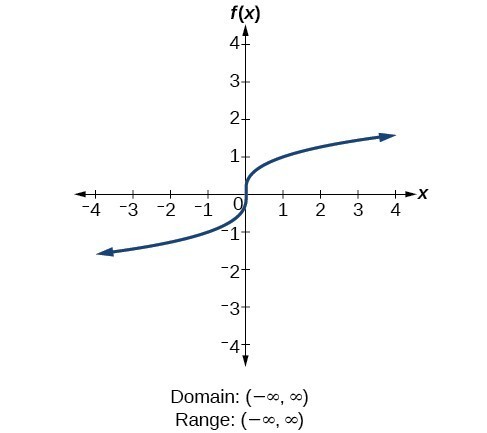



Determine Domain And Range From A Graph College Algebra
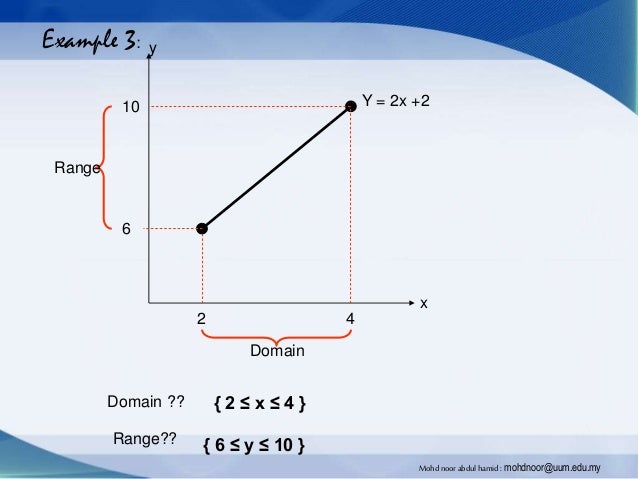



Introduction To Function Domain And Range Mohd Noor




Find Domain And Range Of Function Y 1 X Youtube



How To Find The




How To Graph Logarithms Transformations And Effects On Domain Range Video Lesson Transcript Study Com




How To Find The Domain And Range Of A Function 14 Steps



How Do You Find The Domain And Range Of Y Sqrt 3x 5 Socratic




Domain And Range Of Quadratic Functions Video Khan Academy
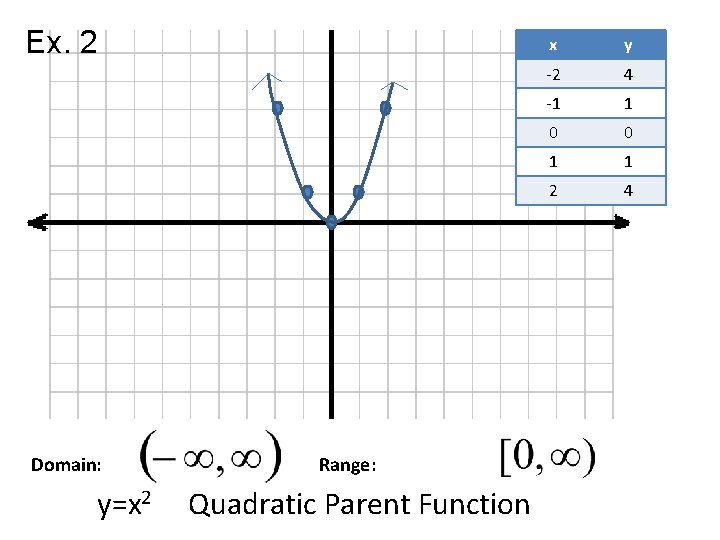



Day 5 Book Section 7 8 Review Parent




Find The Domain And The Range Of The Real Function F X X 3 X 5




Answered Domain Range And Level Curves In Bartleby



Find The Domain And Range Of The Following Relations I R1 X Y X Y N X Y 10 Sarthaks Econnect Largest Online Education Community
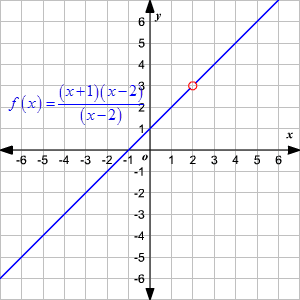



Domain And Range Of Rational Functions



How Do You Find The Domain And Range Of F X X 4 4x 3 3x 2 Socratic




Solved Evaluate The Following Find The Domain And Range Chegg Com
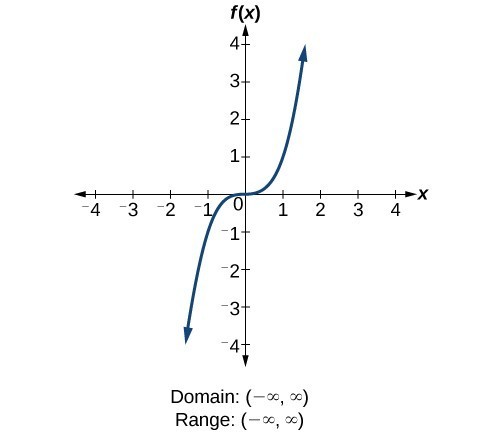



Determine Domain And Range From A Graph College Algebra




Domain And Range Of 2x 3 X 2 A Rational Function Youtube
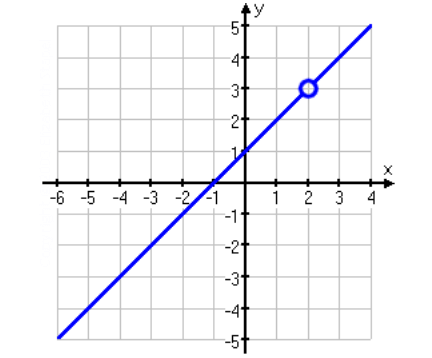



Domain And Range Of Rational Functions With Holes



What Are The Domain And Range For 1 Y X 3 And 2 Y 16 X 2 Quora




How To Find Domain And Range Video Practice Questions




How Do You Find The Domain And Range Of X 3 0 Homeworklib
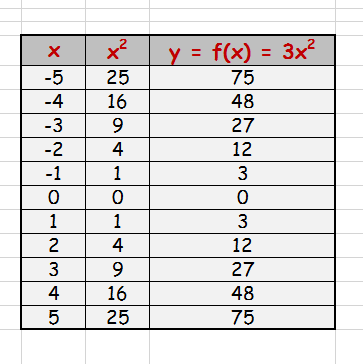



How Do You Find The Domain And Range Of Y 3x 2 Socratic
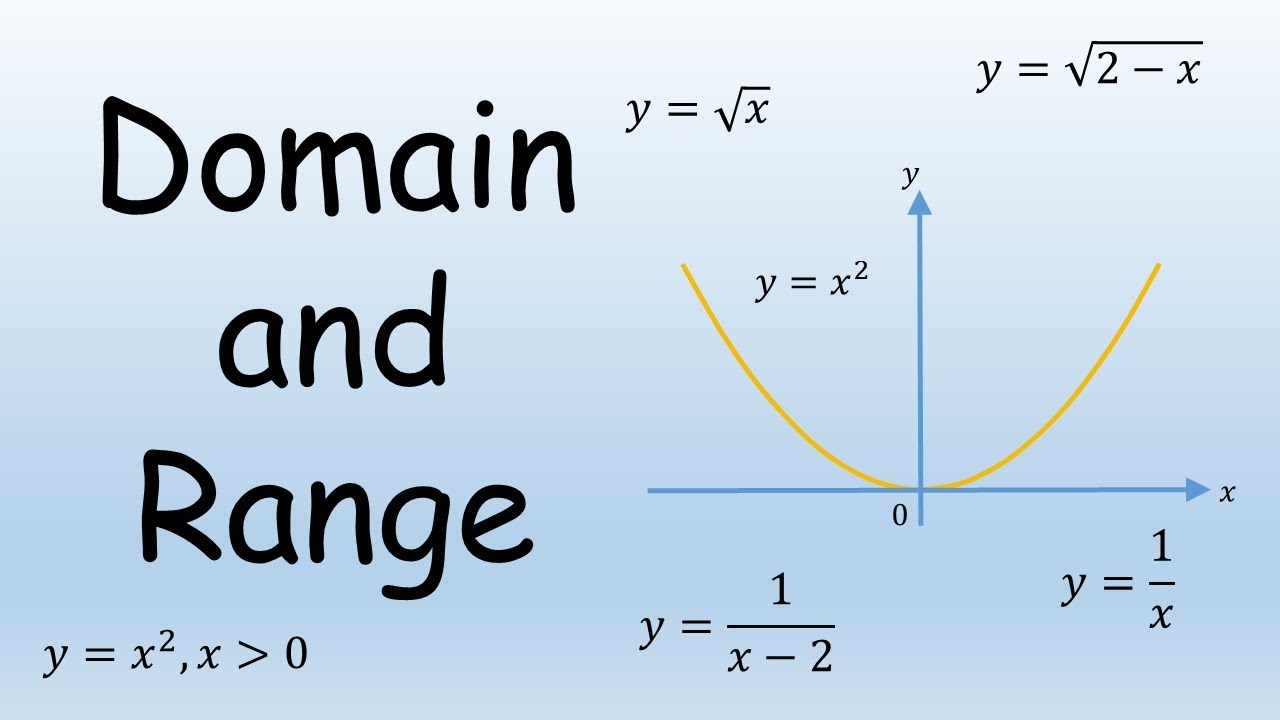



Domain And Range Of A Function Youtube




Let A 1 2 3 14 Define A Relation R From A To A By R X Y 3x Y 0 Where X Y A Write Down Its Domain Co Domain And Range
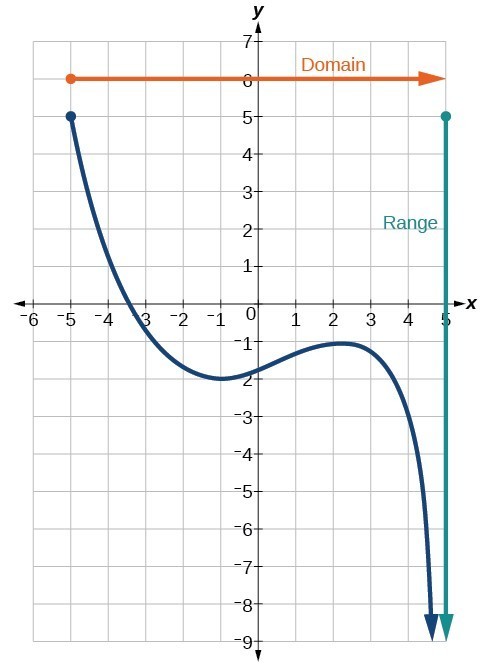



Determine Domain And Range From A Graph College Algebra



Solution This Question Asks To Quot Find The Domain And Range Of Each Function Quot 1 Y X 1 2 Y 1 X 3 Y 1 X 2 1 4 Y 1 Squareroot Of X 2 X 1 Can Someone Please Show Me How To Do
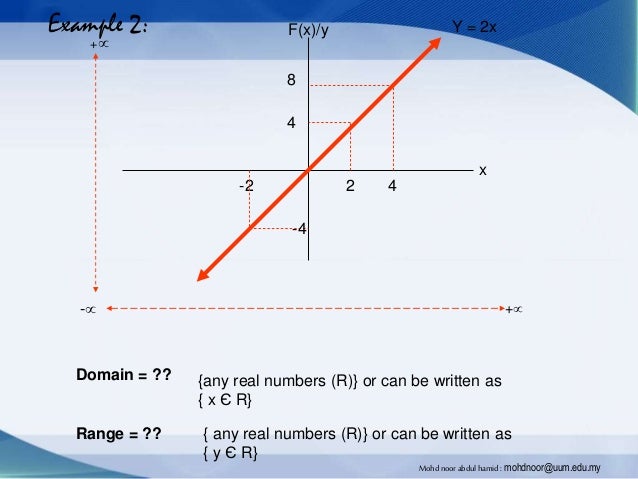



Introduction To Function Domain And Range Mohd Noor



What Is The Domain And Range Of 1 X 3 Quora




Find The Domain And Rangeof Following Functions1 Z 1 Xy2 Z Y X3 Z Y X Whole Under Root Brainly In



1




What Are The Domain And Range Of This Function Y X 3 2 5 Brainly Com




Domain And Range Free Math Help




Domain And Range Ppt Download



Finding Domain And Range
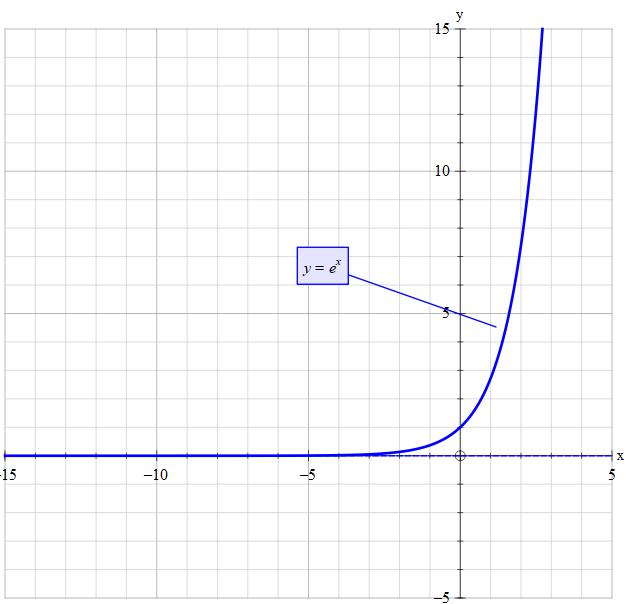



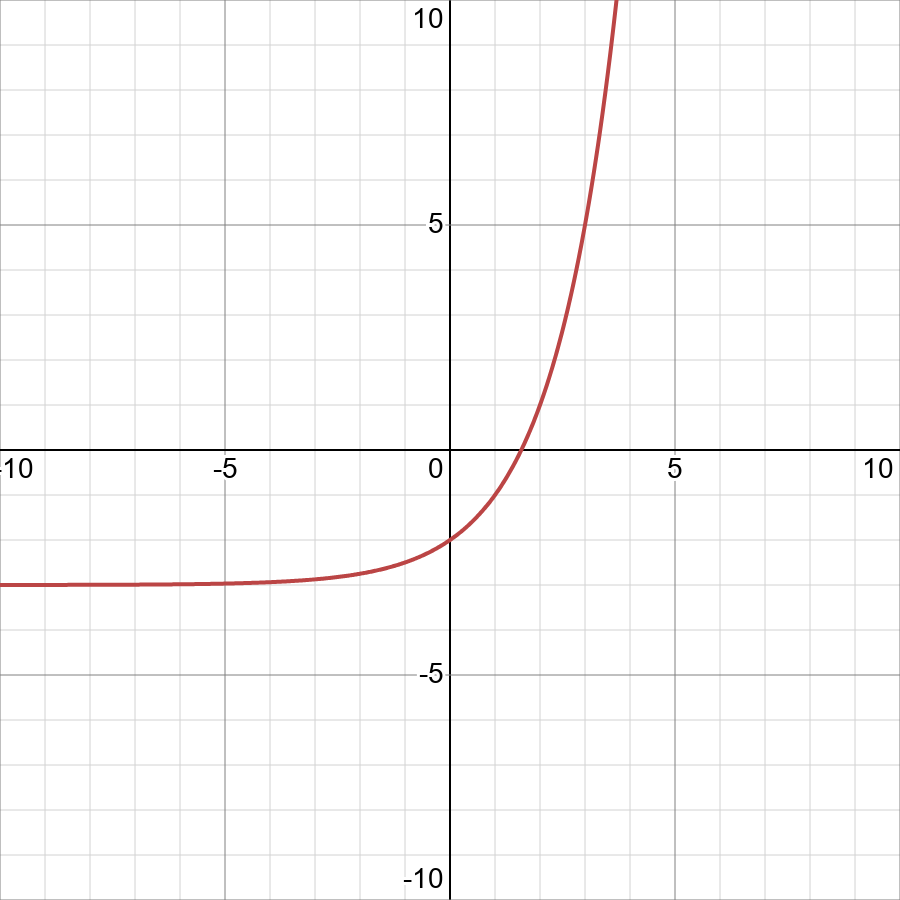
What Is The Domain And Range Of Y E X Socratic
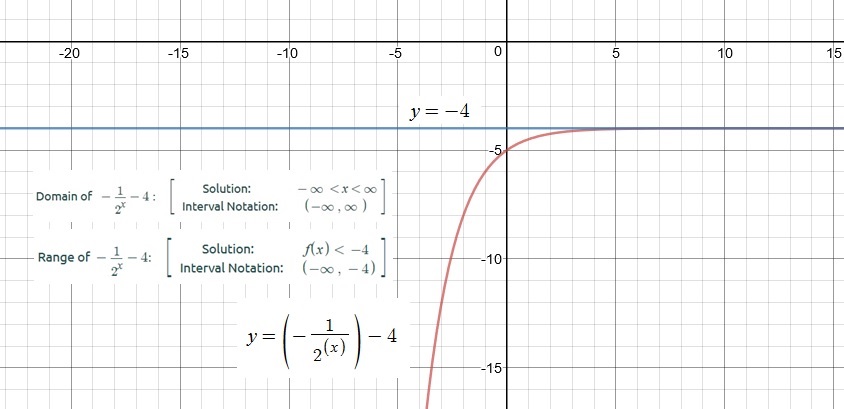



What Is The Domain And Range Of Y 2 X 4 Socratic




Exercise 1 3 Functions Problem Questions With Answer Solution




Domain And Range Free Math Help



Domain And Range



How Do We Draw The Graph And Find The Range And Domain Of The Function F X X 1 Quora



Content Finding Domains And Ranges




How To Graph Y Sqrt X Video Lesson Transcript Study Com



0 件のコメント:
コメントを投稿